Anakent Koleji Fen Kulübü Resmi Sitesi - Bilim Adamlarının Hayatları

Jean-Baptiste de LAMARCK(1744-1829)

Büyük fransız doğa bilimcisi lamarck,ingiliz bilim adamı charles darwin in doğduğu yıl philosophie zoologique adlı ünlü yapıtını yayımlamıstı.

bu yapıtında bazı evrim kurallarını açıklamıstır.fransa nın picardie bölgesindeki bir koyde doğan lamarck çocukluğundan beri asker olmayı düsünürken,babasının isteğine uyarak papaz olmak uzere din eğitimine basladı.ama 1760 da babasının olmesiyle orduya yazıldı ve 7 yıl savaslarında karhamanca carpıstı.sağlığı nedeniyle 1768 de ordudan ayrılmak zorunda kaldı.sonraki yıllarda pariste tıp eğitimi gorurken bir yandanda botanik alanındaincelemeler yaptı ve 1778 da fransanın doğal bitki ortusune ilişkin değerli çalısmalar yayımlayınca fransız bilimler akademisine seçildi.1788 sparis botanik bahçesinde goreve seçildi.

Beş yıl sonra bu kurulus ulusal doğa tarihi müzesi adıyla yeniden örgütlendiğinde zooloji bölümünün yöneticiliğine atanan lamarck o tarihten sonra butun ilgisini zooloji ye yöneltti.bu bilim dalındaki çalısmalarına50 yasından sonra baslamasına ve gozlerinin neredeyse korluk derecesinde bozulmus olmasında karsın bocekler ile solucanlar konusunda en yetkili kişi olarak tanındı.ömrünün son yıllarına doğru da omurgasız hayvanlar biyolojisinin en onemli yapıtlarından birini yayımladı.
-----------------------------------------------------------------------------ALBERT EINSTEIN (1879-1955)

Alman asıllı ABD'li fizikçi Albert Einstein, bütün insanlık tarihinin en büyük bilim adamlarından biridir. Çağdas fiziğin temellerini atan çalısmalarından bugün bile evreni ve evrende gözlediğimiz bütün olayları nasıl yorumlamamız gerektiğine dair yol gösterir.

Yahudi bir ailenin oğlu olan Einstein, Ulm'da doğdu ve Münih'te öğrenime başladı. Okul yıllarında matematiğe özel bir ilgi duyarak bu alanda sivrildi. 15 yaşındayken ailesi İtalya'nın Milano kentine taşınınca Einstein İsviçre'ye geçerek Zürich Teknik Üniversitesi'ne girdi. 1900 de bu üniversitenin kuramsal fizik ve matematik bölümünü bitirdi. Bir süre öğretmenlik yaptıktan sonra Bern'deki patent bürosunda çalışmaya başladı bu görevden arta kalan zamanlarda fizik çalışmalarını sürdürdü ve 1905 te fiziğin gelişmesini sağlayan bir dizi incelemeler yaptı.

Molekül boyutlarının hesaplanmasına ilişkin yeni bir yöntem önerdiği ilk incelemesiyle Zürich Teknik Üniversitesi'nden fizik doktoru ünvanını aldı. İskoçyalı botanikçi Robert Brown'un çiçektozlarında gözlemlediği "Brown hareketi"ne ilişkindi. Brown'ın gözlemlerine göre çiçektozları gibi küçük parçacıklar durgun bir sıvının içinde bile, durmadan hereket ediyordu. Daha önceleri bu olayın rastgele hareket eden sıvı moleküllerinin küçük parçalara çarpmasından olduğu düşünülüyordu. Einstein bu incelemesinde brown hareketin bi matematiksel durum olarak açıkladı.

Einstein'ın üçüncü makalesinde gene yıllar önce keşfedilmiş çok ilginç bir olaya açıklık getiriyordu. Üzerine ışık gönderilen bazı maddelerin elektron yaydığı ama ışığın şiddetini arttığında yayılan elektronların enerjisinde değil yalnızca sayısında artış olduğu biliniyordu. Einstein fotoelektrik etki adıyla bilinen bu olayın açıklamasını yaparken ışığın hem dalgalar halınde hem de enerji yüklü küçük parçacıklar halinde yayıldığını öne sürdü. Bu parçacıklar yani bugünkü adıyla fotonlar maddeye çarptığında atomlardan elektron koparıyor ama serbest kalan elektronlar maddeden kurtulmaya çalısırken atomların çekim kuvvetiyle enerji kaybediyordu. Einstein özellikle bu çalısmasıyla 1921 Nobel Fizik Ödülü'ne değer görüldü.

Einstein aynı yıl yayımlanan dördüncü incelemesi en önemlisidir. Bu makalesinde özel görecelik kuramını 1916 da dahada geliştirerek genel görecelik kuramına ulaşmıştır. Einstein'ın kuramına göre cismin kütlesi,uzunluğu hatta olay süresince zamanın akış hızı cismin hızına bağlı olarak değişir. Bunlar insana inanılmaz gelen devrimci düşüncelerdi ve benimsenmesi çok uzun zaman aldı. Einstein'ın görecelik kuramıyla vardığı en önemli sonuçlardan biri de kütle ile enerjinin eşdeğerliliğidir. Demek ki kütle bir enerji birimi olduğuna göre kütleçekimi de bir kuvvet olarak değil uzayda kütlenin varlığından kaynaklanan bir enerji bandı olarak düşünmek gerekir. Bu nedenle uzaydaki büyük kütleli gökcisimlerinin yakınından geçen ısık ısınlarının doğrultusunda bir sapma olur bu da uzayın eğrilmesine yol açar. Einstein enerji ile kütle arasındaki eşitliği ünlü E=mc2(KARE) bağıntısıyla gösterdi. (E)enerji, (c)ısığın çarpma sayısı, (m) kütle. Işık hızının k****i çok büyük bir sayı olduğundan çok küçük bir kütle çok büyük bir enerjiye eşit olur.

Dünyaca ünlü bir bilim adamı olan Einstein 1914 te Berlin'de kurulan bir arastırma enstütüsünde fizik bölümünün yoneticiliğine getirildi. I. Dünya Savaşı boyunca Almanya'da yasadı ve kararlı barışsever olarak savas karsıtı eylemleri destekledi. 1918 de barışı büyük bir sevinçle karşıladı. Ama 1933 te Nazi Partisi'nin iktidara gelmesi ve yahudilere karşı yürüttükleri eylemler yüzünden artık Almanya'da yaşaması olanaksızdı. Amerika'ya yerleşerek yaşamının sonuna kadar uğraşacağı "Birleşik Alan Kuramı" üstünde çalısmaya basladı. Ne var ki kuvvetle ilişkin bütün fizik kuramlarını tek bir kuramda birleştirmeyi amaçlayan bu çalısmasını sonlandıramadı.

Einstein bütün yaşamı boyunca dünya sorunlarıyla cok yakından ilgilendi. Gerçek bir barışsever olmasına karsın Hitler Almanyasında atom bombası yapmak üzere çalısmalar başladığını öğrenince Almanya ve Japonya'nın böyle bir bombayı kullanmalarını engeller düşüncesiyle atom bombasının ilk kez ABD de yapılmasına ön ayak oldu. Ama II. Dünya Savaşı'nda bu bombaların Hiroşima ve Nagazaki kentlerine atılmasından sonra atom silahının denetlenmesini ve dünya barısının kurulmasını içtenlikle destekledi.

Alçakgönüllü ve sevecen bir insan olan Einstein aynı zamanda bir müziksever ve yetenekli bir kemancıydı.

-----------------------------------------------------------------------------
Anders CELSIUS(1701-1744)

Uppsala da Doğan ve calısmalarını bu kentte gerceklestiren isveçli fizikçi ve astronom anders celsius 1730 da uppsala universitesinde astronomi profösoru oldu.

Yapımi 1740 ta tamamlanan uppsala gozlemevini kurarak yasamının son 4 yılında orada çalıstı.biri dünyanın gunese uzaklıgının hesaplamasına yarayan yeni bir yonteme öburu dünyanın biçimini saptamaya yonelik iki astronomi kitabı yazdı.dünyanın kutuplarda hafifce basık olduğunu gözem yoluyla bulan ilk bilimadamlarından biri oldu.

Celsius günümüzde kendi adını tasıyan sıcaklık olceğinin bulucusu olarak tanınır.sanigrat olarakta adlandırılan bu ölçek dünyanın her yanında özellikle bilimsel olcümlerde kullanılır.daha once kullanılan sıcaklık olceğini Danzigli bir alman fizikçi olan daniel fahrenheit 1714 te geliştirmişti.

Çalısmalarını daha cok hollandada yürüten fahrenheit ın adıyla anılan bu olcek suyun donma noktasını 32F kaynama noktasını 212F olarak gosterir.Celcius 1742 de farklı bir sıcaklık olceği geliştirdi.sıcaklık aralığını 10 esit parcaya boldu.aslında celcius buzun erime noktasını 100 suyun kaynama noktasını 0 olarak kabul etmişti.

Daha sonra 0 ile 100 u yer değiştirdi.baslangıcta bu olceğe yüz adım anlamındaki latince centum gradus tan gelen santigrat ölçeği demişti.ama 1948 de toplanan uluslararası konfreansta adını bulucusunun adı olan celsius la değiştirdiler.celsius derecesi C olarak adlandırılır.

---------------------------------------------------------------------------------

SIR ISSAC NEWTON

Newton (1642 - 1727), tarihin yetiştirdiği en büyük bilim adamlarından biridir ve matematik, astronomi ve fizik alanlarındaki buluşları göz kamaştırıcı niteliktedir; klasik fizik onunla doruğa erişmiştir. Bilime yaptığı temel katkılar, diferansiyel ve entegral hesap, evrensel çekim kanunu ve Güneş ışığının yapısı olarak sıralanabilir. Çalışmalarını Doğa Felsefesinin Matematik İlkeleri (Principia) ve Optik adlı eserlerinde toplamıştır.

Newton, diferansiyel integral hesabı bulmuştur ve bu buluşu 17. yüzyılda ortaya çıkan ve çözümlenmek istenen bazı problemlerden kaynaklanmaktadır.

Bu problemlerden ilki, bir cismin yol formülünden, herhangi bir andaki hız ve ivmesini, hız ve ivmesinden ise aldığı yolu bulmaktı. Bu problem ivmeli hareketin incelenmesi sırasında ortaya çıkmıştı; buradaki güçlük, 17. yüzyılda ilgi odağı haline gelen ansal hız, ansal ivmenin hesaplanması (hızın veya ivmenin bir andan diğer bir ana değişmesini belirlemek) idi.

Örneğin, ansal hız bulunurken, ortalama hız durumunda olduğu gibi, alınan yol geçen süreye bölünerek hesaplanamaz, çünkü verilen bir an içinde alınan yol ve süre sıfırdır; sıfırın sıfıra oranı ise anlamsızdır. Bu biçim hız ve ivme değişimleri diferansiyel hesap ile bulunabilir.

İkinci problem, bir eğrinin teğetini bulmaktı. Bu problem hem bir geometri problemiydi, hem de çeşitli alanlardaki uygulamalarda çok önemliydi. Bu problemlerin çözümü için diferansiyel hesabı uygulamak gerekir.

Üçüncü problem de, bir fonksiyonun maksimum veya minimum değerlerinin bulunması sorunuydu. Örneğin, gezegen hareketlerinin incelenmesinde, bir gezegenin Güneş'ten en büyük ve en küçük mesafelerinin bulunması gibi maksimum ve minimum problemleri ile karşılaşılmaktaydı.

Dördüncü problem ise, bir gezegenin verilen bir süre içinde aldığı yol, eğrilerin sınırladığı alanlar, yüzeylerin sınırladığı hacimler gibi problemlerdi. Bunların çözümleri integral hesap yardımıyla bulunur.

Newton 1665 yılında uzunluklar, alanlar, hacimler, sıcaklıklar gibi sürekli değişen niceliklerin değişme oranlarının nasıl bulunacağı üzerinde düşünmeye başlamıştı. Bir niceliğin diğer birine göre ansal değişme oranını (dx/dy) diferansiyel hesap ile bulmuş ve bu işlemin tersiyle de (integral hesap) sonsuz küçük alanların toplamı olarak eğri alanların bulunabileceğini göstermiştir. Newton, iki mekanik problemin çözümünü bulmaya çalışırken diferansiyel entegral hesabı geliştirmiştir. Bu problemler:

1) Gezegenin hareketi sırasında yörüngesi üzerinde katettiği yoldan, herhangi bir andaki hızını bulmak,

2) Gezegenin hızından, herhangi bir anda yörüngesinin neresinde bulunacağını hesap etmekti.

Bu problemlerin çözümüne hazırlık olarak Newton, y = x2 denkleminde herhangi bir andaki yolu y, ve düzgün bir dx hızı ile alınan başka bir andaki yolu da x ile göstererek, 2xdx'in aynı anda y yolunu alan hızı temsil edeceğini söylemiştir.

Newton diferansiyel-integral hesabı bulduğunu 1669 yılına kadar kimseye haber vermemiş ve ancak 42 yıl sonra yayınlamıştır. Bundan dolayı da Leibniz ile aralarında öncelik problemi söz konusu olmuştur. Leibniz, Newton'dan daha iyi bir notasyon kullanmış, x ve y gibi iki değişkenin mümkün olan en küçük değişimlerini dx ve dy olarak göstermiştir.

1684 yılında yayımladığı kitabında dxy= xdy+ ydx, dxn= nxn-1, ve d(x/y)=(ydx-xdy)/y2 formüllerini vermiştir.

Newton matematiğin başka alanlarına da katkıda bulunmuştur. Binom ifadelerinin tam sayılı kuvvetlerinin açılımı çok uzun zamandan beri biliniyordu. Pascal, katsayıların birbirini izleme kuralını bulmuştu; ancak kesirli kuvvetler için binom açılımı henüz yapılmamıştı. Newton (x-x2)1/2 ve (1-x2)1/2 açılımlarını sonsuz diziler yardımıyla vermiştir.

Principia'da Newton, Galilei ile önemli değişime uğrayan hareket problemini yeniden ele alır. Uzun yıllar Aristoteles'in görüşlerinin etkisinde kalmış olan bu problemi Galilei, eylemsizlik ilkesiyle kökten değiştirmiş ve artık cisimlerin hareketinin açıklanması problem olmaktan çıkmıştı.

Ancak, problemin gök mekaniğini ilgilendiren boyutu hâlâ tam olarak açıklanamamıştı. Galilei'nin getirdiği eylemsizlik problemine göre dışarıdan bir etki olmadığı sürece cisim durumunu koruyacak ve eğer hareket halindeyse düzgün hızla bir doğru boyunca hareketini sürdürecektir.

Aynı kural gezegenler için de geçerlidir. Ancak gezegenler doğrusal değil, dairesel hareket yapmaktadırlar. O zaman bir problem ortaya çıkmaktadır. Niçin gezegenler Güneş'in çevresinde dolanırlar da uzaklaşıp gitmezler?

Newton bu sorunun yanıtını, Platon'dan beri bilinmekte olan ve miktarını Galilei'nin ölçtüğü gravitasyonda bulur. Ona göre, Yer'in çevresinde dolanan Ay'ı yörüngesinde tutan kuvvet yeryüzünde bir taşın düşmesine neden olan kuvvettir. Daha sonra Ay'ın hareketini mermi yoluna benzeterek bu olayı açıklamaya çalışan Newton, şöyle bir varsayım oluşturur:

Bir dağın tepesinden atılan mermi yer çekimi nedeniyle A noktasına düşecektir. Daha hızlı fırlatılırsa, daha uzağa örneğin A' noktasına düşer. Eğer ilk atıldığı yere ulaşacak bir hızla fırlatılırsa, yere düşmeyecek, kazandığı merkez kaç kuvvetle, yer çekim kuvveti dengeleneceği için, tıpkı doğal bir uydu gibi Yer'in çevresinde dolanıp duracaktır

Böylece yapay uydu kuramının temel prensibini de ilk kez açıklamış olan Newton, çekimin matematiksel ifadesini vermeye girişir. Kepler kanunlarını göz önüne alarak gravitasyonu F = M.m /r olarak formüle eder. Daha sonra gözlemsel olarak da bunu kanıtlayan Newton, böylece bütün evreni yöneten tek bir kanun olduğunu kanıtlamıştır. Bundan dolayı da bu kanuna evrensel çekim kanunu denmiştir.

Newton'un diğer bir katkısı da fizikte kuramsal evreyi gerçekleştirmiş olmasıdır. Kendi zamanına kadar bilimde gözlem ve deney aşamasında bir takım kanunların elde edilmesiyle yetinilmişti. Newton ise bu kanunlar ışığında, o bilimin bütününde geçerli olan prensiplerin oluşturulduğu kuramsal evreye ulaşmayı başarmış ve fiziği, tıpkı Eukleides'in geometride yaptığına benzer şekilde, aksiyomatik hale getirmiştir. Dayandığı temel prensipler şunlardır:

1. Eylemsizlik prensibi: Bir cisme hiçbir kuvvet etki etmiyorsa, o cisim hareket halinde ise hareketine düzgün hızla doğru boyunca devam eder, sükûnet halindeyse durumunu korur.

2. Bir cisme bir kuvvet uygulanırsa o cisimde bir ivme meydana gelir ve ivme kuvvetle orantılıdır (F = m.a).

3. Etki tepki prensibi: Bir A cismi bir B cismine bir F kuvveti uyguluyorsa, B cismi de A cismine zıt yönde ama ona eşit bir F kuvveti uygular.

Newton'un ağırlıkla ilgilendiği bir diğer bilim dalı da optiktir. Optik adlı eserinde ışığın niteliğini ve renklerin oluşumunu ayrıntılı olarak incelemiştir ve ilk kez güneş ışığının gerçekte pek çok rengin karışımından veya bileşiminden oluştuğunu, deneysel olarak kanıtlamıştır.

Bunun için karanlık bir odaya yerleştirdiği prizmaya güneş ışığı göndererek renklere ayrılmasını ve daha sonra prizmadan çıkan ışığı ince kenarlı bir mercekle bir noktaya toplamak suretiyle de tekrar beyaz ışığı elde edebilmiştir. Ayrıca her rengin belirli bir kırılma indisi olduğunu da ilk bulan Newton'dur.

---------------------------------------------------------------------------------

GALİLEO GALİLEİ

Adı 17. yüzyıl bilimsel devrimi ile birlikte anılan en önemli bilim adamlarından birisi olan Galileo (1564-1642), fizik, matematik ve astronomi gibi konularda çığır açan çalışmalar yapmış ve ilgisi daha çok hareket üzerinde yoğunlaşmıştı.

Bu alandaki çalışmalarının sonucunda klasik mekaniğin temellerini kurmuş, Güneş merkezli astronomi sisteminin fiziğini geliştirmiştir. Aristoteles'e göre, her hareket onu hareket ettiren bir kuvvet sonucu meydana gelirdi; cisim bu kuvvet kendisini hareket ettirdiği sürece hareket ederdi.

Galilei, günlük gözlemlere uyan bu Aristotelesçi yaklaşımı eylemsizlik prensibi ile yıkmıştır. Eylemsizlik prensibine göre, kendi haline bırakılan cisim, herhangi bir kuvvet etkisinde kalmadığı sürece, durumunu korur, yani hareket halinde ise hareketine, sükunet halinde ise sükunetine devam eder.

Galilei'nin üstü kapalı olarak ifade ettiği, Newton'un ise formüle ettiği bu prensip ile yeni bir hareket kavramı ileri sürülmüş oldu. Buna göre, hareket cisimde bir değişiklik yapmaz; hareket bir durumdur, bir noktadan başka bir noktaya geometrik bir geçiştir; durma da harekete karşıt başka bir durumdur. Durma için kuvvet uygulanması gerekmiyorsa, hareket için de kuvvet uygulanması gerekmez; hareketin hızının değişmesi için ise kuvvet gerekir. Eylemsizlik, içinde bulunduğumuz Dünya'da gözlemlenemez; ancak ideal koşullar altında böyle bir durum meydana getirilebilir. Zaten Galilei'nin deneyleri de düşünce deneyleri idi.

Galilei için gerçek dünya, matematik bağıntıların dünyası, Platon'un deyimi ile idealar dünyası idi. İçinde yaşadığımız dünyayı anlamak için, idealar dünyasından bakmak gerekliydi.

Mükemmel yuvarlaklıktaki toplar, sürtünmesiz düzlemler üzerindeki hareketlerini, yalnızca idealar dünyasında sonsuza dek sürdürürlerdi. Doğa, geometrik harflerle (eğrilerle, dairelerle, üçgenlerle) yazılmış bir kitap gibiydi; doğayı anlamak için bu dili bilmek gerekiyordu.

Hareket, cisimde bir değişiklik meydana getirmediğine göre, cisim aynı anda birden fazla harekete sahip olabilir. Bu hareketler birbirini engellemez ve birleşerek tek bir yörünge izler. Buradan, fırlatılan bir merminin, düzgün doğrusal hareket ile serbest düşme hareketinin bileşkesi olan parabol biçiminde bir yörünge izlediğini göstermiştir.

Galileo'nun hareket konusunda çözüm getirdiği bir diğer konu da serbest düşme hareketi ile ilgilidir. Düşen bütün cisimlerin aynı ivmeye sahip olduğunu göstererek, serbest düşmenin sabit ivmeli bir hareket olduğunu saptamış ve serbest düşmede alınan yolun zamanın k****iyle orantılı olduğunu (S=1/2 gt2) göstermiştir.

Sonuç olarak, Galilei'nin mekanik konusunu matematikselleştir-meyi başardığı söylenebilir. Düzgün ve sabit ivmeli hareketleri tanımlamış ve matematiksel formüllerini vermiştir. Modern hareket kavramını Galilei'ye borçluyuz.

Galilei teleskopu astronomik amaçla kullanan ilk bilim adamıdır. 1609 yılında yaptığı bir teleskopla önemli gözlemler yapmış ve bu gözlemleri Yıldız Habercisi (Siderius Nuntius) adlı kitabında vermiştir.

Onun astronomide yaptığı gözlemler, Güneş merkezli sistemi desteklediği, Aristoteles fiziğinin geçerli olmadığını kanıtladığı için oldukça önemlidir. En önemli gözlemleri Ay ve Güneş gözlemleridir. Ay'da kraterlerin, dağların ve vadilerin olduğunu görmüş ve bunun Ay ile Yer'in aynı maddelerden yapıldığının kanıtı olduğunu söylemiştir.

Güneş'i gözlemlemiş ve Güneş üzerinde bulunan gölgelerin Güneş'in üzerinde yer alan lekeler olduğunu kanıtlamıştır. O zamanlarda, Güneş üzerinde görünen lekelere ilişkin iki açıklama bulunmaktaydı. Bunlardan birincisine göre, bu leke, Merkür'ün Güneş'in önünden geçerken oluşan gölgesiydi. Ancak Galilei bunun olanaksız olduğunu söyler.

Çünkü Merkür'ün Güneş'in önünden geçişi yaklaşık yedi saat sürmektedir, ancak bu lekeler yedi saatten çok daha fazla Güneş'in üzerinde yer almaktaydılar. İkinci açıklamaya göre, bu lekeler, Güneş ve Yer arasında bulunan küçük gökcisimlerine aittir. Oysa, bu lekelerin Güneş üzerinde hep aynı yerde bulunduklarını tespit etmiştir. Eğer bu lekeler, küçük cisimlerin gölgeleri olsalardı, gözlem yerine bağlı olarak, Güneş üzerinde farklı konumlarda olmalıydılar.

Galilei, Orion kümesini gözlemlemiş ve daha önce bulut olduğu varsayılan bu kümenin gerçekte yıldızlardan oluştuğunu bulmuştur. Yine Samanyolu'nun yıldızlardan oluştuğunu tespit etmiştir. Jüpiter'i gözlemlemiş ve Jüpiter'in çevresinde dolanan dört yıldız belirlemiştir.

Bunların Jüpiter'in etrafında dönen uydular olduklarını bulmuş ve Jüpiter'le birlikte uydularını, "adeta minyatür bir Güneş sistemi" olarak tasvir etmiştir. Satürn'ün halkasını gözlemlemiş ancak teleskopu güçlü olmadığı için gezegenin halkasını iki yapışık parça olarak görmüş ve bunları uydu zannetmiştir.

Gezegenin periyodik özelliğinden dolayı halka bir müddet sonra kaybolmuş ve bu parçaları göremeyen Galilei bu olaya çok şaşırmıştır. Onun bu şaşkınlığı sonrasında yazdığı cümleler ilginçtir: "Galiba Satürn onları yedi." Galilei ayrıca Venüs'ü gözlemlemiş ve Venüs'ün safhaları olduğunu tespit etmiştir. Bu gözlem, Copernicus'un ne kadar haklı olduğunun bir göstergesiydi.

Batlamyus sisteminde Venüs, sürekli belli bir uzaklıkta olmalıydı ve sadece hilâl şeklinde görülmeliydi. Oysa gözlemler, Venüs'ün bazen çok yakın bazen de çok uzakta olduğunu göstermekteydi. Ayrıca Venüs, sadece hilâl olarak değil, değişik hallerde de görünmekteydi. Bu ise ancak Copernicus sistemi ile açıklanabilirdi. Bu da Güneş merkezli sistemi doğruluyordu

---------------------------------------------------------------------------------

Charles Darwin

Lamarck gibi türlerin değiştiğini kabul eden bir başka bilim adamı da Darwin'dir. Charles Darwin (1809-1882) Gallapagos Adaları'nda, evcil hayvanlar, özellikle güvercinler üzerinde yapmış olduğu araştırmaların sonuçlarını Türlerin Kökeni adlı eserinde sunmuştur.

Evrim teorisi olarak adlandırılan bu teoriye göre, koşulların değişmesine bağlı olarak canlı ya hemen değişir ya da uzun zaman içinde değişim gösterir. Eğer canlı değişmezse, yaşam şansını kaybeder. ‚ünkü yaşam ilkesi ekonomidir; her şeyin belli bir işlevi vardır ve o işlevi en iyi şekilde yapmak zorundadır; ona uymayan canlı kaybolur.

Eğer yaşam şartları değişmişse, canlının da buna bağlı olarak değişmesi gerekir; aksi taktirde mevcut fakat işe yaramayan bazı kısımlarını ya da organlarını beslemek ve kendi gücünü korumak için kullanacağı besinini gereksiz yere sarfetmek zorunda kalır.

Bu durumda yaşam savaşında başarılı olma şansını zorlar, hatta kaybedebilir. Bundan dolayıdır aynı görevi yapan organın sayısı fazlaysa, bunlar değişime uğrar ya da uzun süre değişmemiş organlar ve nisbeten az gelişmiş, basit canlılar, aynı şekilde, değişime geçirirler.

Canlı değişime konu olduğunda, kollar gibi benzer organları birlikte değişir. Genellikle, canlıdaki küçük gruplar, örneğin çeşitler türlere ve türler cinslere (genus) göre daha kolay değişmek-tedir.

Canlıda iki güç vardır: Doğa koşullarına uymak için en faydalı ve gerekli organları tutup diğerlerini atması, yani doğal eleme ve ataya geri dönme isteği. Genellikle, bu güçlerden birincisi hakim olur ve canlı doğa koşullarına göre değişir, ancak zaman zaman canlıda geriye dönüşler görülebilir. Bu geriye dönüşler bazen 20 nesil sonra bile görülebilmektedir.

Darwin'in canlıda değişimin ne kadar sürede oluştuğu gibi, evrim teorisiyle açıklayamadığı bazı sorular da vardı. Darwin bu soruya kesin bir yanıt vermez; ona göre bu, çok uzun bir zaman kesitini kapsayabilir.

Evrim teorisi zamanında ve daha sonra büyük tepkilere yol açmıştır. Bazı bilim adamları onu desteklerken, bazıları da şiddetle karşı çıkmıştır. Gerek karşı çıkanlar gerekse destekleyenler, teorinin lehinde ve aleyhinde deliller toplarken, biyolojinin gelişmesine de katkıda bulunmuşlar, özellikle embriyoloji, jeoloji, paleoantropoloji ve karşılaştırmalı anatomi konularındaki çalışmalardan delillerle görüşlerini desteklemişlerdir.

Darwin'e karşı olan bilim adamları canlının değişmediğini, türlerin sabit olduğunu kabul etmişlerdir. Onlara göre, değişme söz konusu olamaz; çünkü canlı yeni koşullara uymaya çalışırken, bunu başaramaz ve yok olur.

Örneğin, iklim değişip de ortalık bataklığa dönüştüğünde, canlı uyum sağlayamadan bataklıkta yok olup gider. Bunlar sönmüş türleri meydana getirir. Bunların en güzel delillerini fosiller bize sağlamaktadır.

---------------------------------------------------------------------------------

THOMAS EDISON

İnsanlık tarihinin en büyük mucitlerinden biri olan Thomas Edison, 11 Şubat 1847’de Amerika’nın Ohio eyaletinde dünyaya geldi. Alman – İngiliz asıllı ve Hollanda göçmeni, koltukçu bir babanın ve İskoç asıllı eski bir Öğretmen olan annenin son ve yedinci çocuklarıydı. Babası’nın Milano’da işi bozulunca yedi yaşında Michigan'daki Mich Port Huron’a göç etmek zorunda kalmışlardı. Edison burada orta halli bir ailenin çocuğu olarak büyümeğe başladı ve ilköğrenimine burada başladı.

Fakat başladıktan yaklaşık üç ay sonra algılamasının yavaşlığı nedeniyle okuldan uzaklaştırıldı. Bundan sonraki üç yıl boyunca özel bir öğretmen tarafından eğitildi. Son derece meraklı ve yaratıcı kişiliğe sahip bir çocuk olan Edison, 10 yaşına geldiğinde kendisini fizik ve kimya kitaplarına verdi.

Oniki yaşına geldiğinde ailesine yardım etmek için Port Huron ile Detroit arasında çalışan trende gazete satmaya başlayan Edison, evlerindeki laboratuvarını trenin yük vagonuna taşıyarak, çalışmalarını burada sürdürdü. Bu dönemde Edison; Michael Faraday’ın “Experimental Research in Electricity” adlı yapıtını okudu ve derinden etkilendi.

Bunun üzerine bir yandan Faraday'ın deneylerini tekrarladı bir yandan da kendi deneylerine ağırlık vererek daha düzenli çalışmaya ve notlar tutmaya başladı.

Onbeş yaşına gelince kendi kazandığı tüm parayı bir baskı makinesine yatırdı ve Weekly Herald adlı bir gazete çıkardı. Bu gazetenin yazılarını kendisi trende yazıyor ve evde basıyordu. Ancak bir gün hareket halindeki bir furgona atlarken bir tren memuru tarafından yakalandı. Memur kulağını o kadar çekti ki günlerce kulak ağrısından kıvranmak zorunda kaldı. Ancak bu olay sonradan daha da ilerleyen sağırlığının başlangıcı oldu.

Edison onaltı yaşındayken telgrafçılığı öğrendi ve ve dört yıl boyunca Middle West’te telgraf memuru olarak dolaştı. Bir Mucit olma isteği onda bu yıllarda başladı.

1868'de kendine atölye kurdu ve aynı yıl geliştirdiği elektrikli bir oy kayıt makinasının patentini aldı. Aygıt oldukça ilgi topladı ama kimse tarafından satın alınmadı. Tüm parasını yitiren Edison, Boston'dan ayrılarak New York'a yerleşti. Edison'un şansı altın borsasının düzenlenmesinde kullanılan telgrafın bozulması üzerine döndü.

Borsa yetkililerinin istemi üzerine aygıtı ustaca tamir eden Edison, Western Union Telegraph Company'den geliştirilmekte olan telgraflı kayıt aygıtları üzerinde yetkinleştirme çalışması yapma önerisi aldı. Bunun üzerine bir arkadaşı ile birlikte Edison Universal Stock Printer mühendislik şirketini kurdu. Ve sattığı patentlerle kısa sürede önemli bir servet edindi.

Bu parayla New Jersey'deki Newark'ta bir imalathane kurarak telgraf ve telem aygıtları üretmeye başladı. Bir süre sonra imalathanesini kapatarak New Jersey'deki Menlo Park'ta bir araştırma laboratuvarı kurdu ve tüm zamanını yeni buluşlar yapmaya yönelik çalışmalara ayırdı. Edison’un patentini aldığı 1300’den fazla icadı vardır.

Edison, 1876'da Graham Bell'in geliştirdiği konuşan telgraf üzerinde çalışmaya başladı. Aygıta karbondan bir iletici ekleyerek telefonu yetkinleştirdi. Ses dalgalarının dinamiği üzerine yaptığı bu çalışmalardan yararlanarak 1877'de sesi kaydedip yineleyebilen gramafonu geliştirdi. Geniş yankı uyandıran bu buluşu ününün uluslararası düzeyde yayılmasına neden oldu.

1878'de William Wallace'in yaptığı 500 mum güçündeki ark lambasından etkilenen Edison, bundan daha güvenli olan ve daha ucuz bir yöntemle çalışan yeni bir elektrik lambasını geliştirme çalışmasına girişti. Bu amaçla açtığı bir kampanyanın yardımıyla önde gelen işadamlarının parasal desteğini sağladı ve Edison Electric Light Company'yi kurdu.

Oksijenle yanan elektrik arkı yerine havası boşaltılmış bir ortamda (vakum) ışık yayan ve düşük akımla çalışan bir ampul yapmayı tasarlıyordu. Bu amaçla 13 ay boyunca flaman olarak kullanabileceği bir metal tel yapmaya uğraştı. Sonunda 21 Ekim 1879'da özel yüksek voltajlı elektrik üreteçlerinden elde ettiği akımla çalışan karbon flamanlı elektrik ampulünü halka tanıttı. Üç yıl sonra New York sokakları bu lambalarla aydınlanacaktı.

1879’da Edison bir elektrik ampulü icat etti. Kömürleştirilmiş iplikten Flamanlarla deneyler yaptıktan sonra karbonlaştırılmış kağıt flamanda karar kıldı. 1880’de evde güvenle kullanılabilecek ampuller üreterek tanesini 2,5 dolara satmaya başladı. Ancak 1878 yılında bir İngiliz bilim adamı olan Joseoh Swan da bir elektrik ampulü icat etmiştir. Ampul camdı ve içinde kömürleştirilmiş bir flaman bulunuyordu. Swan, ampulün içindeki havayı boşlattı çünkü havasız ortamda flaman yanıp tükenmiyordu. İşte son olarak da bu iki adam güçlerini birleştirmeye karar vererek Edison ve Swan Elektrikli Aydınlatma Şirketi’ni kurdular.

İki kez evlenerek altı çocuk sahibi olan Edison yaşamının sonuna kadar yeni buluşlar yapmaya devam etti. Geriye çığır açıcı buluşlarını yanı sıra, gözlemleriyle dolu 3.400 not defteri bıraktı.

18 Kasım 1931’de, 84 yaşındayken New Jersey de hayat veda etti.

---------------------------------------------------------------------------------

FARABİ

Felsefenin Müslümanlar arasında tanınmasında ve benimsenmesinde büyük görevler yapmış olan Türk filozoflarının ve siyasetbilimcilerinden Fârâbî'nin, fizik konusunda dikkatleri çeken en önemli çalışması, Boşluk Üzerine adını verdiği makalesidir. Fârâbî'nin bu yapıtı incelendiğinde, diğer Aristotelesçiler gibi, boşluğu kabul etmediği anlaşılmaktadır.

Fârâbî'ye göre, eğer bir tas, içi su dolu olan bir kaba, ağzı aşağıya gelecek biçimde batırılacak olursa, tasın içine hiç su girmediği görülür; çünkü hava bir cisimdir ve kabın tamamını doldurduğundan suyun içeri girmesini engellemektedir. Buna karşılık eğer, bir şişe ağzından bir miktar hava emildikten sonra suya batırılacak olursa, suyun şişenin içinde yükseldiği görülür. Öyleyse doğada boşluk yoktur.

Ancak, Fârâbî'ye göre ikinci deneyde, suyun şişe içerisinde yukarıya doğru yükselmesini Aristoteles fiziği ile açıklamak olanaklı değildir. Çünkü Aristoteles suyun hareketinin doğal yerine doğru, yani aşağıya doğru olması gerektiğini söylemiştir.

Boşluk da olanaksız olduğuna göre, bu olgu nasıl açıklanacaktır? Bu durumda Aristoteles fiziğinin yetersizliğine dikkat çeken Fârâbî, hem boşluğun varlığını kabul etmeyen ve hem de bu olguyu açıklayabilen yeni bir varsayım oluşturmaya çalışmıştır. Bunun için iki ilke kabul eder:

1. Hava esnektir ve bulunduğu mekanın tamamını doldurur; yani bir kapta bulunan havanın yarısını tahliye edersek, geriye kalan hava yine kabın her tarafını dolduracaktır. Bunun için kapta hiç bir zaman boşluk oluşmaz.

2. Hava ve su arasında bir komşuluk ilişkisi vardır ve nerede hava biterse orada su başlar.

Fârâbî, işte bu iki ilkenin ışığı altında, suyun şişenin içinde yükselmesinin, boşluğu doldurmak istemesi nedeniyle değil, kap içindeki havanın doğal hacmine dönmesi sırasında, hava ile su arasındaki komşuluk ilişkisi yüzünden, suyu da beraberinde götürmesi nedeniyle oluştuğunu bildirmektedir.

Yapmış olduğu bu açıklama ile Fârâbî, Aristoteles fiziğini eleştirerek düzeltmeye çalışmıştır. Ancak açıklama yetersizdir; çünkü havanın neden doğal hacmine döndüğü konusunda suskun kalmıştır.

Bununla birlikte, Fârâbî'nin bu açıklaması, sonradan Batı'da Roger Bacon tarafından doğadaki bütün nesneler birbirinin devamıdır ve doğa boşluktan sakınır biçimine dönüştürülerek genelleştirilecektir.

---------------------------------------------------------------------------------

İbn-i Sina (980 - 1037)

Felsefe, matematik, astronomi, fizik, kimya, tıp ve müzik gibi bilgi ve becerinin muhtelif alanlarında seçkinleşmiş olan, İbn Sînâ (980-1037) matematik alanında matematiksel terimlerin tanımları ve astronomi alanında ise duyarlı gözlemlerin yapılması konularıyla ilgilenmiştir.

Astroloji ve simyaya itibar etmemiş, Dönüşüm Kuraminın doğru olup olmadığını yapmış olduğu deneylerle araştırmış ve doğru olmadığı sonucuna ulaşmıştır. İbn Sînâ'ya göre, her element sadece kendisine özgü niteliklere sahiptir ve dolayısıyla daha değersiz metallerden altın ve gümüş gibi daha değerli metallerin elde edilmesi mümkün değildir.

İbn Sînâ, mekanikle de ilgilenmiş ve bazı yönlerden Aristoteles'in hareket anlayışını eleştirmiştir; bilindiği gibi, Aristoteles, cismi hareket ettiren kuvvet ile cisim arasındaki temas ortadan kalktığında, cismin hareketini sürdürmesini sağlayan etmenin ortam, yani hava olduğunu söylüyor ve havaya biri cisme direnme ve diğeri cismi taşıma olmak üzere birbiriyle bağdaşmayacak iki görev yüklüyordu.

İbn Sînâ bu çelişik durumu görmüş, yapmış olduğu gözlemler sırasında hava ile rüzgârın güçlerini karşılaştırmış ve Aristoteles'in haklı olabilmesi için havanın şiddetinin rüzgârın şiddetinden daha fazla olması gerektiği sonucuna varmıştır; oysa meselâ bir bir ağacın yakınından geçen bir ok, ağaca değmediği sürece, ağaçta ve yapraklarında en ufak bir kıpırdanma yaratmazken, rüzgar ağaçları sallamakta ve hatta kökünden kopartabilmektedir; öyleyse havanın şiddeti cisimleri taşımaya yeterli değildir.

İbn Sînâ'ya Aristoteles'in yanıldığını gösterdikten sonra, kuvvetle cisim arasında herhangi bir temas bulunmadığında hareketin kesintiye uğramamasının nedenini araştırmış ve bir nesneye kuvvet uygulandıktan sonra, kuvvetin etkisi ortadan kalksa bile nesnenin hareketini sürdürmesinin nedeninin, kasri meyil (güdümlenmiş eğim), yani nesneye kazandırılan hareket etme isteği olduğunu sonucuna varmıştır.

Üstelik İbn Sînâ bu isteğin sürekli olduğuna inanmaktadır; yani ona göre, ister öze âit olsun ister olmasın, bir defa kazanıldı mı artık kaybolmaz. Bu yaklaşımıyla sonradan Newton'da son biçimine kavuşan eylemsizlik ilkesi'ne yaklaştığı anlaşılan İbn Sînâ, aynı zamanda nesnenin özelliğine göre kazandığı güdümlenmiş eğimin de değişik olacağını belirtmiştir.

Meselâ elimize bir taş, bir demir ve bir mantar parçası alsak ve bunları aynı kuvvetle fırlatsak, her biri farklı uzaklıklara düşecek, ağır cismimler hafif cisimlere nispetle kuvvet kaynağından çok daha uzaklaşacaktır.

İbn Sînâ'nın bu çalışması oldukça önemlidir; çünkü 11. yüzyılda yaşayan bir kimse olmasına karşın, Yeniçağ Mekaniği'ne yaklaştığı görülmektedir. Onun bu düşünceleri, çeviriler yoluyla Batı'ya da geçmiş ve güdümlenmiş eğim terimi Batı'da impetus terimiyle karşılanmıştır.

İbn Sînâ, her şeyden önce bir hekimdir ve bu alandaki çalışmalarıyla tanınmıştır. Tıpla ilgili birçok eser kaleme almıştır; bunlar arasında özellikle kalp-damar sistemi ile ilgili olanlar dikkat çekmektedir, ancak, İbn Sînâ dendiğinde, onun adıyla özdeşleşmiş ve Batı ülkelerinde 16. yüzyılın ve Doğu ülkelerinde ise 19. yüzyılın başlarına kadar okunmuş ve kullanılmış olan el-Kânûn fî't-Tıb (Tıp Kanunu) adlı eseri akla gelir.

Beş kitaptan oluşan bu ansiklopedik eserin Birinci Kitab'ı, anatomi ve koruyucu hekimlik, İkinci Kitab'ı basit ilaçlar, Üçüncü Kitab'ı patoloji, Dördüncü Kitab'ı ilaçlarla ve cerrâhî yöntemlerle tedavi ve Beşinci Kitab'ı ise çeşitli ilaç terkipleriyle ilgili ayrıntılı bilgiler vermektedir.

İslam tarihinde önemli adımların atıldığı bir dönemde bilim hususunda daha sonra gelişecek olan Avrupa biliminde de önemli etkileri olacak olan İbn Sina, geliştirdiği felsefeyle de daha sonraları bir çok İslam alimi tarafından da eleştirilmiştir.

---------------------------------------------------------------------------------
ROBERT BOSCH

Alman sanayici Bosch motorlu araçlar için elektrik donanımı üreten dünya çapında başta gelen firmayı küçük bir tesisatçı dükkanından başlayarak kurdu. 20. yüzyılın başında hemen hemen her otomobile takılan manyetoyu geliştirerek dünya çapında ünlendi.

Bosch Schwaebische Alb dağlarında bir köy olan Albeck'de bir çiftçi ailesinin oniki çocuğunun onbirincisi olarak dünyaya geldi. Ailesinin başlıca gelir kaynağını, arabacıların geceledikleri ve atlarını değiştirdikleri bir han oluşturuyordu.

Tren hattı döşendiğinde ailece Ulm'e taşındılar. Bosch ince tesviyecilik dalındaki çıraklığını tamamladıktan sonra ülkesinden ayrıldı. 1884'te ABD'ye giderek burada Thomas Alva Edison ile birlikte çalıştı ve ardından da İngiltere'ye gitti.

Ondan iki yıl sonra da 10.000 marklık bir sermaye ile Stuttgart'ta bir tesisat, ince tesviyecilik ve elektroteknik şirketi kurdu. 1887'de bir arkadaşının kızkardeşi olan Anna Kayser ile evlenerek iki çocuk sahibi oldu.

Bosch, bir makinacı kalfa ve bir çırak çocukla birlikte her türlü elektrik tesisatı onarıyor ve telefon, ev telgrafı ve paratoner (yıldırımsavar) gibi aygıtları monte ediyordu.

1887'de gazlı motorlar için ürettiği manyetoyu izleyen yıllarda giderek geliştirdi. Elde ettiği başarılar yüzünden tesisatçı firmasının kapasitesini gözünde büyüttü. Yeni makine alımı için fazla yatırım yaptı ve 1890'da parasal sıkıntıya düştü. Ancak 1897'de ekonomik sıkıntısını atlatabildi.

Kendisi tarafından üretilen manyeto artık bir motorlu araca, bir Dioa-Bouton Üç Tekerleklisine takılabildi. Bosch bundan beş yıl sonra kesin başarıya ulaştı. Proje mühendisi Gotdob Honold bujilerle bir yüksek gerilim manyetosu geliştirdi. Bir aygıt ateşleme hızı ve dakiklik açısından tüm rakip firmaların ürünlerinden üstündü.

Ayrıca hızlı çalışan benzinli motorların geliştirilmesi üzerinde etken oldu. Aradan çok geçmeden Bosch hemen hemen bütün büyük otomobil firmalarından sipariş almaya başladı.

Yeni yüzyıla girdikten birkaç ay sonra, bu arada 45 kişi çalıştıran Bosch, Stuttgart'a taşındı. Elektroteknik fabrikasını plânlarken ABD'de edindiği deneyimlerden yararlandı.

Modera iş bölümünü göz önünde tutarak imalathanelerini donattı. Sık sık "Kızıl Bosch" olarak nitelendirilen sanayici, Almanya genelinde ancak 1918'de kabul edilen 8 saatlik iş gününü 1906'da uygulayarak sosyal tutumunu kanıtladı.

1910'da fabrikasında çalışanlara Cumartesileri öğleden sonra izin verdi. Diğer işletmelerin çoğunda o tarihte haftada altı tam gün çalışılıyordu. Şirketi 1913'te 7 haftalık bir işçi mücadelesine sahne olunca, Bosch işverenler birliğine katıldı. O tarihe kadar bu örgüte üye olmayı reddetmişti.

Birinci Dünya Savaşı patlak vermeden önce Bosch ürünlerinin % 90'ını dış ülkelere satıyordu. Şirketi, motorlu taşıtlar için buji, ışık makinesi, akü, starter, far vb. parçalardan oluşan ilk standart elektrikli donanımı sunuyordu.

İngiltere, Fransa ve ABD'de kendi şirketleri ve temsilcilikleri bulunmaktaydı. Her ne kadar savaş başladığında dış ülkelerden sağladığı kazanç elden gittiyse de, savaş için yaptığı üretim bunu kat kat çıkartıyordu. Bosch bu kazancının büyük bir bölümünü Neckar kanalının inşası için kurulan bir vakfa devretti. 1916'da firmasını anonim şirkete çevirdi.

Her zaman teknikteki yenilikleri göz önünde bulunduran Bosch, Birinci Dünya Savaşı sona erdikten sonra araştırmaya büyük paralar ayırdı ve işletmesini giderek büyüttü.

Özel hayatında 20'li yıllarda kaderin birkaç sillesine katlanmak zorunda kaldı. Oğlu mültipl skleroz hastalığından öldüğü gibi, çocuğunun ölümünü kabullenemeyen karısı da geçirdiği ağır depresyonlar yüzünden hastanelerde bakılmak zorunda kaldı. Bosch 1926'de boşandı ve bir yıl sonra Margarete Woerz ile evlenerek bir kız çocuk sahibi oldu.

Yine 1927'de çalışanlara şirkette uzun yıllar çalıştıktan sonra, emekliliklerinde parasal destek sağlayan Bosch Yardımı adı altında toplumsal bir kuruluşu hayata geçirdi. Ne var ki, 30'lı yılların başındaki dünya ekonomik buhranı 1937'den beri Robert Bosch GmbH adını taşıyan bu kuruluşu da etkiledi. Satışlar hissedilir derecede gerilerken çalışanların kimisine yol vermek gerekti.

Bosch' un fabrikaları İkinci Dünya Savaşı'nda geniş çapta yıkıldılarsa da kendisi buna tanık olmadı. Şirketin kurucusu 1942 yılinda 80 yaşında Stuttgart'ta hayata veda etti. Fabrikaları yeniden inşa edildikten sonra üretim yelpazesine buzdolapları ve diğer elektrikli ev aletleri eklendi.

---------------------------------------------------------------------------------

FERDİNAND PORSCHE

Alman otomobil tasarımcısı sonraları "böcek" adı altında dünya çapında satış rekorları kıran KdF- Wagen'i (otomobil) 1935'ten itibaren üretmeye başladı. Porsche, İkinci Dünya Savaşı'ndan sonra ilk spor otomobili geliştirdi.

Porsche, Maffersdorf/Bohemia'da musluk tamircisi bir babanın oğlu olarak dünyaya geldi. Boş zamanlarında teknik ve elektrikle uğraştı. Liseyi bitirdikten sonra Viyana'ya giderek Teknik Üniversiteye dinleyici öğrenci olarak yazıldı. İlk işini elektrik motorları üreten bir işletmede buldu.

Otomobil tutkusunun farkına burada vardı. Lohner-Porsche Porsche 1900'daki Paris Fuarı'nda, kendi buluşu olan ve dingillerindeki elektrik motorlarıyla çalışan otomobili sergiledi.

Taşıt aracını Viyana saray arabaları yapımcısı Lohner şirketinin elemanı olarak yaptığı için, bu yeni otomobil Lohner-Porsche olarak tanındı. Bunun hemen ardından düşüncesini daha da geliştirerek elektrik motorlarını bir benzin motoru aracılığıyla besledi. Bu yeni tahrik biçimiyle şanzıman dişlisine gerek kalmıyordu.

Porsche teknik müdür olarak Viyana Neustadt'taki Austro-Daimler şirketine geçti. Burada tanınmış bir uzun mesafe yarışı olan Prinz-Heinrich-Fahrt için yaptığı otomobille yarışı bizzat kazandı.

Porsche ayrıca uçak motorları ve Birinci Dünya Savaşı'nda topları taşıyan çekici araç tasarımcısı olarak kendisine bir isim yaptıktan sonra, savaşın ardından tasarladığı iki binek otomobiliyle Austro-Daimler'deki son başarılarına imza attı. 1923'te firmanın Stuttgart'taki merkezine teknik müdür ve tasarımcı olarak geçti. Avusturya'daki Steyr şirketinde kısa bir süre (1928-30) çalıştıktan sonra, 55 yaşında bağımsızlığı seçti.

Kendi Şirketi Uluslararası bir şöhrete sahip olan Porsche, yorulmak bilmeksizin daha başka teknik yenilikler de geliştirdi ve çeşitli firmalar için komple yeni otomobiller tasarladı.

Esnekliği dolayısıyla yüklenme halinde dönebilen bir amortisör elemanı olan döner çubuk yaylanıcısını (süspansiyonunu) buldu. Sıkışık parasal durumunu, ardından gelen yıllarda Nasyonal Sosyalist rejimin önemli bir taşıt aracı danışmanı olarak düzeltti. İyi kişisel ilişkilerinin ve ortak çıkarlarının bulunduğu Hitler'in buyruğuyla Porsche, geniş halk kitlelerinin satın alabilecekleri sağlam bir otomobil tasarımına başladı.

Hitler'in diğer koşulları şunlardı: Saatte 100 kilometrelik hız, 4-5 kişilik yer,100 kilometrede en fazla 8 litrelik benzin tüketimi, 1.000 RM'nin (Reichsmark) altında satış fiyatı. 1936'da 4 silindirli Boxer motorlu, 22 beygir güçlü ve 984 cc hacimli ilk 3 test otomobili hazırdı.

Sonradan "Volkswagen" (böcek) olarak adlandırılan hava soğutmalı otomobil, önce Alman İşçi Birliği çerçevesindeki Nasyonal Sosyalist Yardım Kuruluşu "Kraft durch Freude"den (Neşeden güç doğar) esinlenerek "KdF-Wagen" olarak piyasaya çıktı. Porsche genelde bu otomobilin mucidi olarak kabul edildiği halde asıl konstrüksiyon planları, tasarımını 1925'ten itibaren geliştiren ve Porsche'ye 1932'de bunları boş yere öneren Çekoslavakya'lı Bela Barenyi'ye aitti.

Savaş İçin Tasarımlar 1937'de NSDAP'ye (Alman Nasyonal Sosyalist İşçi Partisi) giren Porsche bir yıl sonra SS'e de katıldı. Buna karşın, yalnız işini düşünen ve politikayla ilgisi olmayan bir insan olarak tanındı. Basit bir tasarımcıyken Wolfsburg'daki Volkswagen AG'nin kurucusu ve yöneticisi oldu. Porsche burada "böcek"in seri üretimine başladı.

Yeni teknik gelişmelere tutkun olan Porsche, İkinci Dünya Savaşı'nda askeri araç üretimine ağırlık verdi. Alman Devleti'nin en büyük ulusal onur madalyasını aldıktan sonra "profesör" ünvanını kullanabilen zırhlı araç tasarımcısı olarak ön plana geçti. Ayrıca Volkswagen'i askeri amaçla cip ve yüzer araç haline getirdi. Porsche'nin işletmesi savaşın bitmesine bir yıl kala Gmünd/ Karnten'e nakledildi.

Almanya'nın teslim oluşundan sonra tutuklanan Porsche bir Fransız cezaevinde kaldı. 1947'de kefaletle serbest bırakıldı. Bundan böyle, oğlu Ferry'nin yönetimi altında onarım işleri ve yedek parça üretimiyle ayakta kalmaya çalışan Karnten'deki fabrikasına kendini adadı.

1948'de kendi adı altında tanınan, 40 beygir gücündeki bir VW motoruyla donatılmış olan ilk spor arabasını piyasaya çıkarttı. İşletmesi 1950'de tekrar Stuttgart'a nakledildi ve Porsche burada 75 yaşında öldü.

---------------------------------------------------------------------------------

Johannes Kepler

Babası yoksul bir paralı asker, annesi de bir hancının kızıydı. Başlangıçtan beri bozuk olan sağlığının üç yaşında yakalandığı ve gözleriyle ellerinin zayıf kalmasına neden olan, çicek hastalığından sonra daha da kötüleşmesi nedeniyle ailesi din adamı olarak yetiştirilmesine karar verdi. Çok yoksul bir aileden gelmesine karşın üstün zekasıyla küçük yaşta dikkatleri çeken Kepler, Württemberg dükünün yardımıyla Tübingen Universite'sinde sürdürdüğü öğrenimini 1588 de bitirdi. 1591'de aynı üniversitede lisansüstü çalışmasını tamamladı. Michael Mästlin'in Tübingen'deki astronomi derslerini izleyerek Copernik sistemini benimsemesi Keplerin sonraki yaşamı açısından önemli bir dönüm noktası oldu. Daha sonra başladığı ilahiyat öğreniminin son yılında iken Graz'da ki Lutherci lisede boşalan matematik öğretmenliğine atandı. Böylece ilahiyat öğrenimini bırakmış oldu. 1594'te gittiği Graz'da evrenin yapısına ilişkin araştırmalarına başladı. Platoncu felsefenin ve Pythagorasçı matematiğin etkisiyle evrende var olduğuna inandığı matematiksel uyumu ortaya koymaya çalıştı. Bu amaçla eski yunalılardan beri bilinen ve Platon cisimleri olarak adlandırılan beş düzgün çokyüzlüden yararlanmayı düşündü. Uzay da yalnız bu beş düzgün çokyüzlünün var olabileceği eski yunanlılarca kanıtlanmıştı. Bu beş düzgün çokyüzlü şunlardı. Dörtyüzlü (yüzleri dört eşkenar üçgen olan piramid),küp,sekizyüzlü(sekiz eşkenar üçgen), onikiyüzlü(oniki düzgün beşgen) ve yirmi yüzlü(yirmiş eşkenar üçgen). Bu çok yüzlüler köşelerinden geçen birer küre içine yerleştirilebildikleri gibi bunların içine yüzlerine orta noktalarından teğet olacak biçimde birer küre yerleştirilebilir. Copernik astronomisi her biri bir küre üzerinde dolanan altı gezegen tanıyordu. Kepler bu altı gezegenin üzerinde dolandığı kürelerin aralarında beş ploton cismi bulunacak biçimde iç içe yerleşmiş durumda olduklarını öne sürdü. Kepler 1600'de, o sıralarda imparatorluk matematikçiliğine atanan Tycho Brahe'nin yanına gitti ve onun asistanı oldu. Brahe ertesi yıl ölünce imparatorluk matematikçiliğine atandı. Kepler yıldızların insanların yaşamlarını yönlendirdiği yolundaki boş inancı redetmesine karşın, evren ile insan arasında belirli bir uyum olduğuna inanıyordu ve astrolojiye dayanan öngörüleriyle ün yapmıştı. Tycho Brahe'nin araştırma grubunda Kepler'e Mars'ın incelemesi görevi verilmişti. Ama o önce ışığın atmosferde kırılması olgusunu incelemek gerektiği kanısına vardı. Dış uzaydaki gökcisimlerinden gelen ışık ışınlarının, Yeri çevreleyen yoğın atmosfere girdiklerinde nasıl kırıldığı konusundaki araştırmalarının sonuçlarını Ad vitellionem Paralipomena Quibus Astronomiae Pars Optica Traditur(astronomideki optik konuların incelenmesi konusunda Vitellio'ya ek) gibi alçakgönüllü bir başlık altında yayımladı.Brahe'nin gözlem sonuçlarını dairelerden oluşan ve düşünebildiği her türden yörünge biçimine uydurmaya çalışıp başarıya ulaşamayan Kepler, Kopernik'in görüşlerinden de esinlenerek, dairesel olmayan yörüngeleride ele aldı. Ve doğru sonuca ulaştı. Mars odaklarından birinde Güneş bulunan eliptik bir yörüngede dolanıyordu. Gezegenler yörüngede dolanırken eşit zaman aralıklarında eşit yol almıyordu ama gezegeni güneşe birleştiren doğru parçası eşit zaman aralıklarında eşit alanlar tarıyordu Bu iki yasa bügün Kepler'in birinci ve ikinci yasası olarak bilinir. Keplarin üçünçü yasası ise Gezgenlerin güneşe olan ortalama uzaklıklarının üçünçü kuvveti , yörüngedeki dolanma sürelerinin k****iyle orantılıdır. Bu üç yasa yarım yüzyıl sonra Isaac Newton'un evrensel kütle çekimi yasasını bulmasında belirleyici rol oynamıştır.

-----------------------------------------------------------------------
Nicolas Copernicus

Copernik modern astronominin kurucusu olarak bilinir. Polonya'da doğdu. Cracow üniversitesine gönderildi. Burada matemetik ve optik üzerine çalıştı. Italya' da amcasının zorlamasıyla akademik yaşamının geri kalan günlerini geçireceği Frauenburg katedraline rahip olarak atandı. Bu pozisyonundan dolayı gücünün doruğuna erişti. Fakat sürekli öğrenci olarak kaldı. Boş zamanlarında resim yaptı ve yunan şiirlerini latinceye çevirdi. Onun astronomiye zaten var olan merakı giderek bir numaralı ilgi alanı oldu. O araştırmalarını kendi başına ve yardım almadan yaptı. Gökyüzünü kathedralin duvarları içindeki bir kuleden gözlemledi ve bu gözlemleri teleskop'un icadına yüzlerce yıl kala çıplak gözle gerçekleştirdi. 1530'da dünyanın kendi ekseni etrafında günde bir kere , güneşin etrafında yılda bir kere döndüğünü iddia ettiği büyük çalışması De Revolutionibus'u bitirdi. Bu o zamanlar inanılmaz birşeydi. Copernik'e kadar, batı dünyası evrenin gerisinde hiçbirşey olmayan kapalı ve küresel bir yapıda olduğunu iddia ettiği Ptolemiac teorisine inanıyordu. O zamana kadar düşünürlerin hemfikir olduğu Claudius Ptolemy Alexandra'da yaşayan bir Mısırlı'ydı. Potelmy'e göre dünya; sabit, hareketsiz ve evrenin merkezine konumlandırılmış güneş dahil herşey onun etrafında dönmekte idi. Bu insan doğasına çekici gelen bir teoriydi. İnsanın günlük gözlemlerine ve egosuna uygun düşen birşeydi. Copernik teorisini yayımlamakta acele etmedi. Teorinin birkaç astronom arasında incelenerek, kendisine fikir verebileceğini düşündü. Copernik' in çalışmaları, eğer genç bir adam bu çalışmaları 1939'da incelememiş olsaydı hiçbir zaman basılacak duruma gelemeyebilirdi. 66 yaşındaki bir rahibin yazısını okuyup ilgilenen 25 yaşındaki Alman Profesör George Rheticus 'du. Copernik'in çalışmalarıyle birkaç hafta ilgilenmeyi tasarladı ama,iki yıl boyunca teori üzerine çalıştı ve teoriden çok fazla etkilendi. O zamana kadar Copernik teoriyi yayımlamakta isteksizdi. Kilisenin teorisi hakkında ne söyleyeceği ile çok ilgilenmesede o herşeyin mükemmel olmasını isteyen ve 30 yıl teori hakkında çalışmasına rağmen hiçbir zaman tamamlanmadığını düşünen biriydi. Copernik için gözlemler sürekli tekrar edilmeliydi(Ilginç olan dünyanın 300 yılının kaybına yolaçan elyazmaları 19. yüzyıl ortalarında Prag'da bulundu. Bu yazmalar gösterdi ki Copernik teorisini sürekli gözden geçiriyordu. Bu yazmaların hepsi o zamanlar için bilgili kişilerin kullandığı latince ile yazılmıştı.) Copernik 1543'de öldü ve hiçbir zaman çalışmalarının nasıl bir sansasyon yarattığını göremedi. Ortaçağdan kalma filozofik ve dinsel inanışlara karşı geldi. Copernik teorisi insanın, evrenin kendisi için yaratılmadığını, yalnızca onun bir parçası olduğunu düşünmeye zorladı. Onun çalışmalarının en önemli yanı insanın Cosmos' a bakışını değiştirmiş olmasıdır

---------------------------------------------------------------------

Stephen Hawking

Stephan Hawking 8 ocak 1942'de (Galileo'nun doğumundan tam 300 yıl sonra) Ingiltere Oxford'da doğdu.Ailesi kuzey Londra'da oturuyordu.Fakat II. dünya savaşı sırasında burası bebek dünyaya getirmek için çok emniyetli bir yer değildi. Bu yüzden Oxford'a taşındılar. Hawking sekiz yaşında iken, kuzey Londra'dan 20 mil uzaktaki St Albans gitti.Onbir yaşında St Albans okuluna kayıt oldu.

Buradan mezun olduktan sonra babasının eski okulu Oxford üniversite' si kollejine devam etti.

Stephan babasının tıpla ilgilenmesini istemesine karşın, o matematiği seviyordu. Fakat okulun matemetik bölümü mevcut değildi. Bu yüzden onun yerine fizik okumaya başladı. Üç yıl sonra doğa bilimlerinde birinci sınıf onur madalyasıyla ödüllendirildi.

Stephan daha sonra Cosmology üzerine çalışmak üzere Cambridge' e gitti. O zamanlar Oxford' da Cosmology üzerine çalışma yoktu. Cambridge'de Fred Hoyle'u supervisor olarak istemesine karşın süpervisorü Denis Sciama idi. Doktorasını aldıktan sonra ilk önce araştırma asistanı, daha sonra Gonville' de Caius kollejde profesör asistanı oldu. 1973'de Astronomi Enstütüsünden ayrıldıktan sonra Stephan uygulamalı matematik ve teorik fizik bölümüne geçti. 1979'dan sonra matematik bölümünde Lucasian profesörü oldu. Bu profesörlük 1663 yılında üniversite parlemento üyesi olan Henry Lucas tarafından kurulmuştu. Ilk olarak Isaac Barrow sonra 1669'da Isaac Newton'a verilmişti.

Stephan Hawking, evrenin temel prensipleri üzerine çalıştı. Roger Penrose ile birlikte Einstein'in Uzay ve Zamanı kapsayan Genel görecelik teoreminin Big Bang'le başlayıp karadeliklerle sonlandığını gösterdi. Bu sonuç Quantum Teorisi ile Genel Görecelik Teorisinin birleştirilmesi gerektiğini ortaya koyuyordu. Bu yirminci yüzyılın ikici yarısının en büyük buluşlarından biriydi. Bu birleşmenin bir sonucuda karadeliklerin aslında tamamen kara olmadığını, fakat radyasyon yayıp buharlaştıklarını ve görünmez olduklarını ortaya koyuyordu. Diğer bir sonucda evrenin bir sonu ve sınırı olmadığıydı. Buda evrenin başlangıcının tamamen bilimsel kurallar çercevesinde meydana geldiği anlamına geliyordu.

Onun birçok kitabından bazıları, The Large Scale Structure of Spacetime, General Relativity: An Einstein Centenary Survey, ve 300 Years of Gravity. Stephen Hawking'in en popüler ve ençok satan iki kitabı; A Brief History of Time ve daha sonraki kitabı, Black Holes and Baby Universes and Other Essays.

Profesör Hawking 12 onur derecesi almıştır. 1982'de CBE ile ödüllendirilmiş,bundan başka birçok madalya ve ödül almıştır. Royal Society'nin ve National Academy of Sciences (Amerikan ulusal bilimler akademisi(N.A.S.) ) üyesidir.

O teorik fizik çalışmaları ve yüklü programına rağmen ailesine (üç çocuk ve bir torun) her zaman zaman ayırmayı bilmiştir.

---------------------------------------------------------------------

Ernest Rutherford

Babası araba tamiri ile uğraşan ve çiftçilik yapan Rutherford, ailenin on iki çocuğunun ikincisiydi. Çiftliklerinde çalışır, hemen her konuda babasına yardım ederdi; fakat okulda da başarılıydı. Hatta, Yeni Zelanda Üniversitesi’nin verdiği burslardan birini kazanıp, yüksek öğrenimini sınıf dördüncüsü olarak tamamladı. Rutherford, üniversitedeyken fiziğe duyduğu büyük ilgiyi bir de manyetik radyo dalgaları yakalayıcısı geliştirerek gösteriyordu. Buluşların günlük yaşama uygulanmalarıyla ilgilenmezdi.

Cambridge Üniversitesi’nden burs kazandığı 1895 yılı, onun için bir dönüm noktası oldu. Verilen bursu birincilikle kazanan sınıf arkadaşı, ülkesinden ayrılmak istemediği için, ikinci sıradaki Rutherford, bu mutlu rastlantı ile bilim dünyasına kazanılıyordu. Aslında o yıl, Cambridge Üniversitesi’nin diğer üniversitelerin başarılı öğrencilerine ilk kez burs vermesi, Rutherford’un talih kapısını aralıyordu. Bursa haberi Rutherford’a ulaştığı zaman, tarlada patates söktüğü, bel küreğini bir kenara fırlatarak ‘artık bunları kim sökerse söksün’ dediği, hatta evlilik düşüncesinden de vazgeçip İngiltere’ye gittiği söylenir.

Rutherford, Cambridge’de, J.J. Thomson’ın gözetiminde çalışıyordu. Hocası sesini ayarlayamayan, kaba tavırlı, fakat elleri son derece becerikli son derecece becerikli bu taşralı genci kısa sürede benimsiyordu. Bu, deneylerinde dağınık ve onu bunu deviren, döken Thomson için önemli bir yardım sayılırdı. Rutherford kısa bir süre, Kanada McGill Üniversitesi’nde kalıyor, evlenmek için Yeni Zelanda’ya gidiyor ve çalışmalarını sürdürmek için yeniden İngiltere’ye dönüyordu.

Becquerel’in yakın izleyicisi Rutherford, yeni ve ilginç bir konu olan radyoaktivite alanında çalışmaya başlıyor, Curie’lerle ışıyan maddelerin yaydıkları ışınların birkaç çeşit olduğuna inanıyordu. Artı yüklü olanlara ‘Alfa’ ve eksi yüklü olanlara ‘Beta’ ışınları diyordu. Bu adlar ogün de kullanılıyordu, ancak ikisi birden ‘Hızlandırılmış Parçacıklar’ olarak ifade ediliyorlardı. 1900 yılında kimi ışımaların manyetik alandan etkilenmediği bulununca, Rutherford, bunların elektromanyetik dalgalardan oluştuklarını gösteriyor ve ‘Gama Işınları’ adını veriyordu.

Rutherford önce Soddy ile birlikte, sonra yalnız başına Crookes’un, uranyumun ışıma sonucu başka bir maddeye dönüştüğünü gösteren öncü araştırmalarını sürdürüyordu. Uranyum ve Toryum üzerinde kimyasal işlemler yaparak ve ışımanın ne olacağı merakı ile Rutherford ve Soddy bu elementlerin, ışıma sonucu bir takım ara maddelere dönüştüklerini gösteriyorlardı. Hemen hemen aynı günlerde, Amerika’da Boltwood da bu gözlemleri doğruluyordu. Soddy bu çalışmaları daha da ilerleterek ‘İzotop’ kavramını ortaya atıyordu.

Farklı her ara element, belli bir sürede miktarının yarısını kaybedecek bir hızla parçalanıyordu. Rutherford bu süreye ‘Yarı Ömür’ diyordu. 1906 ile 1909 yılları arasındaki sürede Rutherford ve yardımcısı Geiger, alfa parçacıklarını derinliğine inceliyorlar, bu parçacıkların elektronlarını kaybetmiş Helyum atomu olduğunu, hiçbir kuşkuya yer vermeyecek biçimde gösteriyorlardı. Alfa parçacıklarının Goldstein’in bulduğu artı yüklü ışınlara benzedikleri anlaşılıyor ve 1914 yılında Rutherford, en basit artı yüklü ışınların Hidrojen’den elde edilenler olması gerektiğini ileri sürerek, artı yüklü temel parçacık niteliklerinden dolayı ‘Proton’ adını kullanıyordu. Bundan sonraki yirmi yıl süresince her atomun eşit sayıda proton ve elektrondan oluştuğuna inanılıyor; fakat bugün kabul edilen yapısıyla hidrojen atomunun bir protonu olduğunu Heinsenberg gösteriyordu. Bugünkü bilgilere göre, proton artı; elektron eksi yüklüdür ve elektriksel olarak bir elektron, bir protonu dengeleyecek biçimde eşit yüklüdürler. Fakat protonun kütlesi, elektronun 1836 katıdır.

Alfa parçacıklarına duyduğu ilgi, Rutherford’u daha önemli şeylere yöneltiyordu. 1906 yılında daha Kanada’nın McGill Üniversitesi’ndeyken, ince madensel levhaların alfa parçacıklarını nasıl dağıttığını incelemişti 1908 yılında İngiltere’ye döndüğünde Manchester Üniversitesi’nde de bu deneyleri sürdürüyordu. Yarım mikron kalınlığındaki bir altın levhaya alfa parçacıkları gönderiyor ve parçacıklardan çoğunun hiç etkilenmeden ve yön değiştirmeden aradaki fotoğraf plakasına kayıtlandıklarını görüyordu. Fakat fotoğraf üzerinde, hem de büyük açılarla kimi dağılımlar oluyordu. Altın levha, 2000 atom kalınlığında olduğu ve alfa parçacıklarının çoğu dağılmadan arkadaki fotoğraf plakasına geçtiklerine göre, altın atomlarının büyük bir bölümü boşluktan oluşmalıydı. Kimi alfa parçacıkları, yönlerinden çok kesin biçimde;hatta 90 derece saptıklarına göre, atomun bir yerinde artı yüklü, alfa parçacıklarını saptırabilecek güçte (benzer yükler itişirler) büyük kütleli bir bölge bulunmalıydı. Rutherford bu deneye dayanarak, çekirdekli atom kuramını ilk 1911 yılında açıklıyor, atomun merkezinde, bütün protonları kapsayan ve hemen hemen kütlesinin tamamını oluşturan çok küçük bir çekirdek bulunduğunu ileri sürüyordu. Atomun dış bölgesinde, çok hafif ve görünürde alfa ışınlarının geçmesini engellemeyen eksi yüklü elektronlar yörüngedeydiler.

Bu atom fikri, 23 yüzyıl düşüncelere egemen olan Demokritus’un ‘maddenin en küçük parçası’ görüşünü yıkıyor ve gerçeklere daha çok uyan yeni bir model oluşturuyordu. Elementlerin ışıyarak ayrışması kuramı, alfa parçacıklarının yapıları üzeindeki çalışmaları, çekirdekli atom modeli Rutherford’a 1908 yılı Nobel Kimya ödülü kazandırıyordu. Başarıları bu kadarla kalmıyor, ilk kez Crookes tarafından düzenlenen ışıldama sayacını, yayılan ışınım (radyasyon) miktarını ölçmek için kullanılıyordu. Çinko sülfit bir ekran üzerindeki parıltıları sayarak (her atom parçasına karşılık bir parıltı) Rutherford ve Geiger, bir gram radyumun saniyede 37 milyar alfa parçacığı saldığını söyleyebiliyorlardı. Bu kadar büyük sayıda alfa parçacığı saçarak parçalanan maddelere, Curie’leri onurlandırmak için, o maddenin ‘Curie’si’ deniyordu. Bu arada Rutherford da unutulmuyor, saniyedeki bir milyon parçalanmaya ‘Rutherford’ adı veriliyordu.

Bu çeşit parıldamalar daha sonra saniyede kullanılıyor ve eser miktarda radyum içerikli çinko sülfit saatlere yerleştiriliyor, rakamların karanlıkta da görülüp okunması sağlanıyordu. Fakat bu saatlerin üretiminde çalışan işçilerin radyum hastalığına tutulmaları nedeniyle, uygulamaya bir süre sonra son veriliyordu.

Daha sonraları Rutherford, içine oksijen, hidrojen ve azot gazları doldurduğu bir silindirde ışıma miktarını ölçmeye girişiyor, azot gazında parıldamaların azaldığını; fakat hidrojen türünden olanların belirdiğini gözlüyordu. O halde alfa parçacıkları, azot atom çekirdeğinden protonlar çıkarıyordu. Çekirdekte kalan da oksijen atom çekirdeği olmalıydı. Böylece Rutherford, kendi ellerini kullanarak bir elementi diğerine dönüştüren ilk insan oluyordu. Başka bir deyişle, simyacıların rüyalarını gerçekleştiriyordu. Bu aynı zamanda, çekirdek tepkimesinin yapay ilk örneği oluyordu. Fakat 300 bin alfa parçacığından ancak biri çekirdek ile tepkimeye girdiği için, bir maddenin diğerine dönüştürülmesinde kolayca uygulanabilir bir yöntem sayılmıyordu.

Rutherford, İkinci Dünya Savaşı’ndan önceki yıllarda amansız bir Nazi düşmanı oluyor, bir çok Yahudi bilim adamının Almanya’dan kaçırılması işlerine karışıyor; fakat zehirli gazlar üzerindeki çalışmaları nedeniyle Haber ‘e ilgi göstermiyordu. Rutherford atomun parçalanmasıyla elde edilen enerjinin denetim altına alınıp kullanılamayacağını söylüyor, Einstein kuramlarına inanmıyordu. Hahn’ın fizyon yöntemi ile enerjiyi nasıl denetim altına alabildiğini görüp tahminlerindeki yanılgıyı anlayamadan, yaşamını yitiriyor ve Newton ile Kelvin’in yanlarına gömülüyordu.

-----------------------------------------------------------------

Charles Augustin de Coulomb

Batı Hint adalarında dokuz yıl askeri mühendis olarak çalışan Coulomb, sağlığının bozulması üzerine Fransa'ya döndü. Fransız devrimi patlak verince Blois'da küçük bir malikhaneye çekilerek tüm zamanını bilimsel araştırmalara ayırdı. 1802 'de halk eğitimi müfettişliğine getirildi.

Coulomb, kendi adıyla anılan yasayı, Ingiliz fizikçi Joseph Priestley'nin elektrik yüklerinin birbirini itmesine ilişkin bulgularını incelemek amacıyla başlattığı çalışmaları sonucunda geliştirdi. Bu amaca yönelik olarak, Priestley yasasında belirtilen elektrik kuvvetlerini ölçmeye yarayan duyarlı aygıtlar yaptı ve elde ettiği sonuçları 1785-1789 arasında yayımladı. Ayrıca benzer ve zıt kutupların birbirini itmesi ve çekmesine ilişkin ters kare yasasını buldu. Bu yasa Siméon-Denis Poisson'u geliştirdiği matematiksel magnetik kuvvetler kuramının temelini oluşturdu. Coulomb, makinelerdeki sürtünmeye, yeldeğirmenlerine, metal ve ipek elyafların esnekliğine ilişkin araştırmalarda yaptı.

----------------------------------------------------------------

Sir Joseph John Thomson

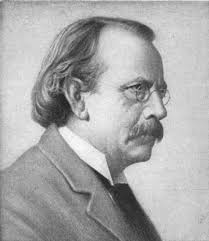
Joseph John Thomson 18 aralık 1856'da Manchester varoşlarından Cheetham Hill'de doğdu. 1870'de Owens College ve 1876'da Trinity College, Cambridge' e burslu olarak girdi. 1880'de Trinity College'e akademi üyesi seçildi .Hayatı boyuncada akademi üyesi olarak kaldı. Daha sonra Lord Rayleigh'ın yerine Cambridge'e deneysel fizik profesörü oldu. 1884-1918 yılları arasında Cambridge ve Royal Institution'ın onursal profesörlüğüyle onurlandırıldı. Thomson'un ilk inceleme konusu ona 1884'de Adams ödülünü kazandıran, Treatise on the Motion of Vortex Rings adlı yapıtında bahsettiği, atomun yapısı üzerineydi. Onun, Application of Dynamics to Physics and Chemistry ve Notes on Recent Researches in Electricity and Magnetism adlı yapıtları, 1886 ve 1892 yıllarında yayımlandı. Bu son çalışması James Clerk Maxwell'in ünlü Treatise adlı yayımından sonra Maxwell'in üçüncü cildi olarak anılır. Ayrıca Thomson, Profesör J. H. Poynting 'le dört ciltlik Properties of Matter adlı ders kitabında işbirliği yaptı. Ve 1885 yılında Elements of the Mathematical Theory of Electricity and Magnetism 'i yayımladı. Thomson, 1896 yılında Princeton Universite' sine son çalışmalarını özetleyen dört konferans vermek için gitti. Bu konferanslar daha sonra Discharge of Electricity through Gases (1897) ismiyle yayımlandı. Amerika'dan dönüşünde hayatının en görkemli çalışmasını gerçekleştirdi. Bu çalışma 30 şubat 1897'de Royal Institution 'daki konferansında açıklayacağı, elektronun keşfiyle sonuçlanan Cathode ışıması idi. Onun 1903 'de yayımlanan Conduction of Electricity through Gases adlı kitabı, Rayleigh tarafından Thomson'un Cavendish Laboratuvarı' ndaki çalışmalarının bir gözden geçirmesi olarak nitelendirilmiştir. Bu yayımın daha sonraki basımını kardeşiyle birlikte iki cilt olarak 1928 ve 1933 yıllarında yayımladı. Thomson, 1904 yılında Yale Universite 'sinde elektrik üzerine altı konferans vermek için geri döndü. Bu konferanslar atomun yapısı üzerine bazı önerilerde bulunuyordu. Thomson, faklı atom ve molekülleri ayrıştırmak için bir yöntem geliştirdi. Bu yöntem daha sonra Aston, Dempster ve diğerleri tarafından birçok izotop'un bulunmasına yol açtı. Yukarıda bahsedilenler dışında, The Structure of Light (1907), The Corpuscular Theory of Matter (1907), Rays of Positive Electricity (1913), The Electron in Chemistry (1923) and his autobiography, Recollections and Reflections (1936), adlı yayımlarıda bulunmaktadır. 1884 yılında Royal Society üyeliğine seçildi. Ve 1916-1920 yılları arasında başkanlığını yaptı. 1894-1902 yıllarında Royal ve Hughes Madalyalarını, 1914 yılında Copley Madalyasını aldı. 1902'de Hodgkins Madalyası (Smithsonian Institute, Washington) ;1923'de Franklin Madalyası ve Scott Madalyası (Philadelphia), 1927'de Mascart Madalyası (Paris), 1931'de Dalton Madalyası (Manchester),ve 1938'de Faraday Madalyası (Institute of Civil Engineers) aldı. British Association 'nın 1909'da başkanlığını yaptı. Ve Oxford, Dublin, London, Victoria, Columbia, Cambridge, Durham, Birmingham, Göttingen, Leeds, Oslo, Sorbonne, Edinburgh, Reading, Princeton, Glasgow, Johns Hopkins, Aberdeen, Athens, Cracow ve Philadelphia Universite'lerinden doktora diploması aldı. 1890'da Rose Elisabeth ile evlendi. Bir oğulları oldu. 30 Ağustos 1940 yılında öldü
---------------------------------------------------------------------------------

Niels Bohr

Atomun yapısı üzerindeki çalışmaları ve atomların saçtığı ışın araştırmaları ile tanınır.
Babası fizyoloji profesörü olan Bohr, 18 yaşında Kopenhag Üniversitesi’nde fizik tahsiline başladı. İyi bir futbolcuydu. Daha iyi bir oyuncu küçük kardeşi 1908 yılının dünya ikincisi Danimarka olimpiyat takımında yer aldı.

26 yaşında doktorasını da tamamlayan Bohr, ileri eğitim bursuyla Cambridge’e gönderildi. Burada elektron kuramcısı J.J. Thomson ile ve daha sonra Manchester’de onun öğrencisi ve yine atom kuramcısı Rudherford ile çalıştı. 27 yaşında beş oğlu olduğu söylenen bir evlilik yaptı. 31 yaşında, fizik profesörü atandığı Kopenhag Üniversitesi’ne döndü.

Rudherford, çekirdekli atom kavramını; yani merkezinde ağır çekirdek bulunan çevresinde daha hafif, bulutsu elektronların dolaştığı bir atom modelini ortaya atmıştı. Atomların nasıl enerji verdiklerini bu model ve Planck’ın on yıl kadar önce yayınladığı kuantum kuramı ile açıklıyordu. Elektronlar gittikçe daralan yörüngeler çizerek çekirdek etrafında dönüyor ve bu hareketleri enerji oluşturuyorlardı. Bohr, daralan yörünge ve sonuçta çekirdek üzerine düşen elektronların varolduğunu kabul etmiyordu.

Atom modeli için daha inandırıcı bir biçim ararken Balmer’in hidrojen tayfı formülü onu, hidrojen atomunu daha yakından incelemeye yöneltti. Hidrojen atomu Lorentz’in belirlediği salınımdayken elektromanyetik ışınım yapmıyordu. Aslında Maxwell’in yasaları temel alındığında, böyle bir ışınım yapması gerekiyordu. Maxwell’e göre, kapalı bir yörüngede kaldıkları sürece ışınım olmayacağı görüşündeydi. Bu çelişkinin nedeni, elektronun sadece bir tanecik kabul edilmesinden ileri geliyordu. Nitekim De Broglie, elektronun yalnız tanecik değil, dalga boyu özellikli de olduğunu gösterince çelişki giderildi. Schrödinger de elektronun çekirdek etrafında dönmediği, yalnızca çevrede durağan bir dalga oluşturduğu görüşüyle, ileri sürülenleri doğruluyordu.

Bohr,”Elektron,yörüngesini değiştirip çekirdeğe yaklaşınca, ışıma olur” diyordu. Fakat, ışın soğuran atomda da elektron çekirdekten daha uzak bir yörüngeye giriyordu. Bu nedenle, elektromanyetik ışınım, bu parçacıkların salınım veya hızlanmalarından değil; enerji düzeylerindeki değişmelerden ileri gelmeliydi. Bu düşünce, atom dünyasının insanın yaşadığı dünyaya benzemediğini gösteriyor, her geçen gün atomun yapısını sağduyu ile açıklamak güçleşiyordu.

Sağduyu, örneğin gezegenlerin yörünge değiştirmediklerini söylüyordu. Elektron da, öyle herhangi bir yörüngeye giremezdi. Ayrıca, her yörünge değişmez bir enerji karşılığı idi. Eğer elektron bir yörüngeden diğerine geçiyorsa,saldığı veya soğurduğu enerji sabit olmalıydı. Bu miktar, kuantumların tümü demekti.Böylece, Planck’ın kuantum kuramı, elektronların atom içinde durum değiştirmeleri olarak yorumlanıyordu.

Hatta Bohr, hidrojen tayfındaki çizgilere karşılık olan enerji yörüngelerini seçebiliyordu.Bununla, bir elktronu bir yörüngeden, çekirdekten daha uzak bir yörüngeye aktaracak miktardaki enerji kuantasının soğurulduğunu gösteriyordu. Özellikle, ilk kez Balmer’in dikkatleri çektiği hidrojen tayfındaki düzgünlük de açıklanabiliyordu.Elektronların belli enerjilerini hesaplayabilmek için Bohr, Planck’ın sabitesini 2*3,14 ile bölerek kullanıyordu.

Bütün bunlara karşılık, tayf çizgilerinin ince ayrıntılarını açıklamak için Bohr’un kullandığı model yetersiz derecede karmaşıktı. Yörüngelerin yalnız dairesel olduklarını varsayıyor; fakat bu, Summerfield’in beyzi yörüngeler varsayıldığında durumun ne olacağı araştırmasını başlatıyordu. Sonuçta, değişik yörüngelerin kabul edilmesi zorunluluğu ortaya çıktı. Yapılması gerekli düzeltmeler bir yana; Bohr’un modeli atom tayfındaki çizgilerin ilk başarılı açıklaması oldu veya tayf çözümlemeleri ile atomların iç yapıları öğrenildi. Fakat yaşlı kuşağın tamamı, bu gelişmeleri benimsemiyordu. Rayleigh, Zeeman ve Thomson kuşku içindeydiler. Ancak, Bohr’un her zaman minnettar kaldığı Jeans, ondan yana çıkıyordu. Aslında Thomson’un karşı çıkmaları nedeniyle, Bohr ondan ayrılmış ve Rutherford ile çalışmayı yeğlemişti.

Kuşkusuz sonuçta Bohr ezici bir başarı sağladı ve 1922 yılı Nobel Fizik Ödülü’nü aldı. Bunu izleyen yıllarda, ikisi de Nobel Fizik Ödülü alan Franck ve Hertz, deneysel çalışmalarıyla Bohr kuramını doğruladılar. Bohr, hidrojenden daha karışık atom modellerini bir türlü geliştiremiyor ve “Birden fazla elektronun bulunduğu atomlarda iç içe küreler vardır. Herhangi bir elementin kimyasal özelliklerini belirleyen en dış küredeki elektron içeriğidir” diyerek çok küreselliğe ilk işaret edenlerden biri oluyordu. Bu düşünce Pauli sayesinde meyvesini verdi. Elektronun hem parçacık (bohr’un fikri) hem dalga (Schrödinger’in düşüncesi) olarak tanımlanması, 1927 yılında Bohr’u, bugün “tümlerlik” diye bilinen ilkeyi önermeye zorladı. Bu, bir şeyin birbirinden tamamen bağımsız; fakat her ikisi de kendi koşullarında geçerli, iki değişik biçimde kabul edilmesi ilkesidir.

1920-1930 döneminde Bohr, bir özel bira şirketinin desteğinde Atom Çalışmaları Enstitüsü’nü Kopenhag’da kurup yöneterek, (Joule zamanından beri bira sanayinin kuramsal fiziğe en büyük katkısı) burayı kuramsal fiziğin merkezi yaptı ve bilimsel yetenekleri Kopenhag’da toplayarak adeta yeni bir “İskenderiye” oluşturdu. 1933 yılında Hitler Almanya’da iktidara gelince, korku içindeki meslektaşları yararına elinden geleni yaptı, özellikle Yahudi fizikçilerin güvenliğini sağladı. Bir toplantı için 1939 yılında Amerika Birleşik Devletleri’ni ziyareti sırasında Hanh’ın “Uranyum, nötronlarla (on yıl kadar önce Chadwick’in bulduğu yüksüz dolayısıyla nötron adı verilen parçacık) bombardıman edilirse parçalanır (fission)” düşüncesini Lisse Meitner’in açıklayacağını söylemesi üzerine toplantı dağıldı ve bilim adamları bu düşünceyi sınamak üzere ülkelerine döndüler. Daha sonraları bu düşünce doğrulandı ve olaylar hızla gelişerek atom bombasında doruk noktasına ulaştı.

Bohr, fisyon sürecine ait bir kuram geliştirmeye koyuldu. Bunda atom çekirdeğinin sıvı damlası gibi davrandığını varsayıyordu. Bohr, bu modelden yararlanarak, birkaç yıl önce Dempster’in bulduğu uranyum 235 izotopunun fisyona uğradığı sonucuna vardı ve bu çıkarımı kısa süre sonra doğrulandı.

Danimarka, 1940 yılında işgal edilince Chadwick’in önerisine uyarak ve bin bir güçlükle İsveç’e kaçtı, böylece muhakkak bir tutuklanmadan kurtuldu. Orada faaliyetlerini genişleterek, çoğu Yahudi bilim adamının Hitler’in elinden kurtulmasını sağladı. Sonra küçük bir uçakla İngiltere’ye geçerken yüksekten uçmak zorunluğu, neredeyse oksijensiz kalıp ölümüne sebep olacaktı. Danimarka’dan ayrılmadan önce Franck ve Lane’nin kendisine emanet ettikleri Nobel madalyalarını da birlikte aldı (kendi madalyasını da Finli savaş kurbanlarına yardım için hibe etmişti) ve asit dolu bir şişeye doldurarak Nazilerin elinden kurtardı.

1945 yılında Amerika Birleşik Devletleri’ne geçerek Los Alamos’daki atom bombası projesinde çalıştı. Atom bombasının sonuçları hakkındaki endişeleri ve uluslar arası denetim amacıyla atom sırlarının bütün müttefiklerce paylaşılması isteği Winston Churchill’i neredeyse tutuklanmasını emredecek kadar kızdırmıştı. Savaştan sonra Kopenhag’a döndü, asitte erittiği altını çöktürerek madalyaları yeniden döktürdü ve sahiplerine ulaştırdı. Bohr, atom enerjisinin barışçı amaçlarla kullanılması için durmadan, yorulmadan uğraştı ve 1955 yılında Cenova’da ilk “Barış için Atom Toplantısını” düzenledi. Bu çabaları da “Barış için Atom” armağanı ile ödüllendirildi.

-----------------------------------------------------------------------------

Michael Faraday

Fraday'ın babası Ingiltere'nin kuzeyinden 1791 başında Newington köyüne iş aramak amacıyla gelmiş bir demirci idi. Annesi Faraday'ın zorluklarla dolu çocukluk döneminde ona duygusal yönden büyük destek olmuş, sakin ve akıllı bir köylü kadındı.Babaları çoğu zaman hasta olan ve iş bulmakta zorluk çeken Faraday ve üç kardeşinin çocukluğu yarı aç yarı tok geçti. Aile Sandemancılar adlı küçük bir hıristiyan tarikatının üyesiydi.

Faraday yaşamı boyunca bu inançtan güç almış, doğayı algılama ve yorumlamada bu inancın etkisi altında kalmıştır. Faraday çok yetersiz bir eğitim gördü. Bütün eğitimi kilisenin pazar okulu'nda öğrendiği okuma yazma ve biraz hesaptan ibaretti. Küçük yaşta gazete dağıtıcısı olarak çalışmaya başladı. 14 yaşında çiftci çıragı oldu. Ciltlenmek üzere getirilen kitapları okuyarak bilgisini genişletmeye başladı. Encyclopedia Brtanica'nın üçüncü baskısındaki elektrik maddesinden özellikle etkilendi. Eski şişeler ve hurda parçalardan yaptığı basit bir elektrostatik üreteçten yararlanarak deneyler yapmaya başladı. Gene kendi yaptığı zayıf bir Volta pilini kullanarak elektrokimya deneyleri gerçekleştrdi.

Londra'daki Kraliyet Enstütüsü'nde Sir Humphrey Davy tarafından verilen kimya konferansları için bir bilet elde etmesi Faraday'ın yaşamında dönüm noktası oldu. Konferanslarda tutduğu notları ciltleyerek iş isteyen bir mektupla birlikte Davy'ye gönderdi. Bir süre sonra laboratuvara yardımcı olarak giren Faraday, kimyayı çağının en büyük deneysel kimyacılarından biri olan Davy'nin yanında öğrenmek fırsatını elde etmiş oldu. 1820'de Faraday, Davy'nin yanından yardımcılık görevinden ayrıldı. Hans Christian Orsted, 1820'de bir telden geçen elektrik akımının tel çevresinde bir magnetik alan oluşturduğunu bulmuştu. Fransız fizikci Andre Marie Ampere tel çevresinde oluşan magnetik kuvvetin dairesel olduğunu gerçektede tel çevresinde bir magnetik silindir oluştuğunu gösterdi. Ve bu buluşun önemini ilk kavrayan Faraday oldu.

Soyutlanmış bir magnetik kutup elde edilebilir ve akım taşıyan bir telin yakınına konursa telin çevresinde sürekli olarak bir dönme hareketi yapması gerekecekti. Faraday üstün yeteneği ve deneysel çalışmadaki ustalığıyla bu görüşü doğrulayan bir aygıt yapmayı başardı. Elektrik enerjisini mekanik enerjiye dönüştüren bu aygıt ilk elektrik motoru idi. Faraday bu deneyleri gerçekleştrip sonuçlarını bilim dünyasına sunarken elektriğin farklı biçimlerde ortaya çıkan türlerinin niteliği konusunda kuşkular belirdi. Elektrikli yılan balığının ve öteki elektrikli balıkların saldığı, bir elektrostatik üretecin verdiği bir pilden yada elektromagnetik üreteçten elde edilen elektrik akışkanları birbirinin aynı mıydı? Yoksa bunlar farklı yasalara uyan farklı akışkanlar mıydı? Faraday araştırmalarını derinleştirince iki önemli buluş gerçekleştirdi.

Elektriksel kuvvet kimyasal molekülleri, o güne değin sanıldığı gibi uzaktan etkileyerek ayrıştırmıyordu, moleküllerin ayrışması iletken bir sıvı ortamdan akım geçmesiyle ortaya çıkıyordu. Bu akım bir pilin kutuplarından gelsede, yada örneğin havaya boşalıyor olsada böyleydi. Ikinci olarak ayrışan madde miktarı çözeltiden geçen elektrik miktarına dorudan bağımlıydı. Bu bulgular Faraday 'ı yeni bir elektrokimya kuramı oluşturmaya yöneltti. Buna göre elektriksel kuvvet, molekülleri bir gerilme durumuna sokuyordu. 1839'da elektriğe ilişkin yeni ve genel bir kuram geliştirdi. Elektrik madde içinde gerilmeler olmasına yol açar. Bu gerilmeler hızla ortadan kalkabiliyorsa gerilmenin ard arda ve periyodik bir biçimde hızla oluşması bir dalga hareketi gibi madde içinde ilerler. Böyle maddelere iletken adı verilir.

Yalıtkanlar ise parçacıklarını yerlerinden koparmak için çok yüksek değerde gerilmeler gerektiren maddelerdir. Sekiz yıl boyunca aralıksız süren deneysel ve kuramsal çalışmaların sonunda 1839'da sağlığı bozulan Faraday bunu izleyen altı yıl boyunca yaratıcı bir etkinlik gösteremedi. Araştırmalarına ancak 1845'te yeniden başlayabildi. 1855'ten sonra Faraday'ın zihinsel gücü azalmaya başladı.Ara sıra deneysel çalışmalar yaptığı oluyordu. Kraliçe Victoria bilime büyük katkılarını göz önüne alarak Faraday'a Hampton Court'ta bir ev bağışladı.

-------------------------------------------------------------------------------------

James Chadwick

Atomun parçalarından nötronu bulmasıyla tanınır.

İyi bir ilk ve orta eğitimden sonra Manchester üniversitesi fizik bölümünden 20 yaşında mezun oldu. Verilen bir burstan yararlanarak ve Geiger ile çalışmak amacıyla Almanya’ya gitti. Almanya savaşa girince bir at ahırına kapatıldı. Fakat çeşitli Alman fizikçilerinin yardımlarıyla 1919 yılında İngiltere’ye dönüp araştırmalarına başladı. Rutherford ile birlikte çeşitli elementlerin alfa parçacıklarıyla bombardımanı üzerinde çalıştı.

Bu deneylerden elde ettiği verileri atomların çekirdekleri üzerindeki artı yükün hesabında kullandı. Aldığı sonuçlar Moseley’in geliştirdiği atom numaraları kuramına uyuyordu.

1920 yılında atomun iki parçacığı olduğu biliniyordu: J.J. Thomson’un bulduğu elektron ve Rutherford’un keşfettiği proton. Protonların tamamı çekirdekteydi. Ama çekirdek atom kütlesinin çoğunu oluşturacak sayıda proton içeriyorsa yükü büyük bir artı değerde oluyordu. Örneğin, helyumun dört protonluk bir kütlesi vardı fakat yükü iki proton karşılığı idi. O halde, çekirdekte geri kalan iki protonluk yükü giderecek birkaç elektron bulunmalıydı. Fakat elektronlar çok hafif parçacıklar olduklarından kütleyi etkileyemezlerdi. Hatta elektronlar, protonları bir arada tutan “çimento” gibi düşünülüyordu. Çünkü elektron olmadan aynı yükteki protonların bir arada duramayıp ayrılacakları sanılıyordu. Bu görüşe göre, helyum çekirdeğinde dört proton ve iki elektron bulunmalıydı ki kütlesi dört ve yükü net artı iki olsun.

Fakat fizikçilerin çoğu bu elektronlu çekirdekten rahatsız oluyor, yüksüz bir parçacığın varlığından şüpheleniyorlardı. Bu düşüncelerle Chadwick ve Rutherford gizemli parçacığı aramaya koyuldular fakat sonuç alamadılar. Güçlük, yüksüz parçacıkların hava moleküllerini iyonlaştırmamasıydı. Çünkü atomun parçacıklarının kolayca saptanması bu iyonlaştırma sayesinde mümkün oluyordu.

1930 ve 1932 yıllarında Bothe ve Joliot-Currie’lerin yaptıkları deneyler, berilyum gibi hafif elementlerin alfa parçacıklara tutulması sonucu ışınma tespit ettiler. Bu, parafinden protonlar yayılmasından anlaşılıyordu. Fakat hiç kimse bu olayı açıklayamadı.

Chadwick bu araştırmaları yeni deneyler yaparak sürdürdü. Ona göre akla yakın tek açıklama, alfa parçacıklarının berilyum atomu çekirdeğinden yüksüz parçacıkları çıkardığı ve bu yüksüz parçacıkların da (her biri bir proton kadar kütleli) parafinden protonları dışarı atmasıydı. Böylece, varlığından şüphelenilen yüksüz parçacık nötronu, bulmuş oldu.

Daha sonraki araştırmalar nükleer tepkimelerin başlamasında büyük rolü olduğunu gösterdi. Buluşunun bu önemi dolayısıyla Chadwick 1935 yılı Nobel fizik ödülünü aldı. O zamanlar uranyum fizyonunun da nötron sayesinde başladığı henüz bilinmiyordu. Üç yıl sonra Hahn ve Meitner bunu da bulup Chadwick’in buluşunun önemini bir daha gösterdiler.

Nötronun bulunmasıyla artık atom çekirdeğinde elektron bulunduğu görüşü geçersiz oldu. Fakat bu kez Heisen Berg, çekirdeğin proton ve nötrondan oluştuğunu ileri sürdü, yani helyum çekirdeği iki proton ve nötron içeriyor böylece kütlesi dört ve yükü de artı iki oluyordu. Belli bir elementin izotopları hep aynı sayıda proton içeriyor dolayısıyla çekirdek çevresindeki elektron sayıları da eşit oluyordu. Elementlerin kimyasal özelliklerinin elektronların sayı ve dizilişlerine bağlı olduğu anlaşıldı. İzotoplar ise aynı elementin değişik sayıda nötron içermesi sonucu oluşuyorlardı. Örneğin, iki cins klorin atomundan biri 17 proton ve 18 nötronla 35 kütleli ve diğeri de 17 proton ve 20 nötronla 37 kütlelidir. Onun için birine klorin 35 ve diğerine klorin 37 denilmektedir. Bütün bu buluş ve çalışmalarla 20 yıl kadar önce Soddy ve Asfon’un ortaya koydukları “izotoplar kuramı” bilimsel temele kavuşmuş oldu.

Çekirdeğin proton ve nötrondan oluştuğu sonucuna varılması biri dışında bütün kuşkuları gidermişti. Fakat hepsi artı yüklü parçacıkları bu kadar dar bir yerde tutan neydi? Bu soruyu cevaplandırmak için üç yıl sonra sonuçlanacak Yukawa’nın çalışmalarının sonuçlarını beklemek gerekiyordu.

İkinci Dünya Savaşı sırasında ve Meitner’in fizyon olayını açıklamasından hemen sonra fakat Amerika’nın el atmasından çok önce, Chadwick İngiltere’nin Atom Bombası Projesi’nin başına geçti ve önemli çalışmalar yaptı

---------------------------------------------------------------------------------

Andre Marie Ampere

Elektrik akım şiddeti birimine adını veren Fransız Matematik ve Fizik Profesörü André - Marie Ampère’dir. Ampère’in deneysel araştırmaları manyetizmanın yeni teorilerini ve elktrodinamiğin esaslarını oluşturmuştur.

Elektrik akım şiddeti uluslararası birim sisteminin temel büyüklüklerinden biri ve elektrik yükü taşıyıcılarının akı yoğunluğunu gösteren bir ölçüdür. Bunun birimi kısaltılmış olarak A ile gösterilen Amper’dir. Bu birime adını veren, elektrik akımı ile manyetizma arasındaki ilişkiyi tespit ederek, elektrodinamiğin temelini oluşturan Matematik ve Fizik Profesörü Fransız André - Marie Ampère’dir.

Elektrik akımı biriminin tarifi için içinden elektrik akımı geçen iletkenleri birbirlerine çeken veya iten kuvvetten yararlanılır:

1 Amper (A), vakum içine paralel olarak yerleştirilmiş, birbirleri ile aralarında 1 metre (m) aralık bulunan, doğrusal olarak sonsuza kadar uzanan, çapları ihmal edilebilecek kadar küçük yuvarlak kesitteki iletkenlerden zamana bağlı olarak değişmeden akan akımın, her metresinde (m), 0,2 mikronewton’luk (µN) bir kuvvet oluşturan akım miktarıdır.

André - Marie Ampère, 22 Ocak 1775’de Lyon/Fransa’da bir tüccarın oğlu olarak dünyaya geldi. Hiç okula gitmedi. Lyon yakınlarında Poleymieux’deki evlerinde, babası tarafından eğitildi. Bu arada Ampère çağdaş ve klasik eserleri de okuyarak kendini daha da geliştirdi. Babası oğlunun matematik yeteneğini farkedince, onu bu yönde teşvik etti. Ampère 12 yaşında A. Euler ve Bernoulli’yi, 18 yaşında Lagrange’ın Analitik Mekaniğini okudu. Babası, 1793 yılında ihtilal çılgınlıkları arasında idam edildi. Bu Ampère için ilk kader şokuydu. 1800 yılında oğlu dünyaya geldi. Aynı yılda, Bourg Departement okulunda Matematik öğretmenliği görevine getirildi.1803 yılında karısı öldü. Bu onda derin bir depresyon yaratan ikinci bir kader şoku oldu. Ampère aynı yıl içinde Lyon Lyceum’unda ve doğa bilimleri dersleri Profesörü olarak göreve başladı ve 1804 yılında Paris Ecole Polytechnique’de Repetitor (müzakereci) ünvanını aldı ve Collegè de France’da Matematik ve Fizik Profesörü olarak dersler verdi. 1808 yılında Napoleon, Ampère’i yaşamının sonuna kadar tüm Fransa’da seyahat etmesini gerektiren bir göreve, Üniversiteler Genel Müfettişliği’ne atadı. Bu arada Tarih ve Felsefe Fakültesi’nde felsefe dersleri de veriyordu. 1809 yılında Titular Profesör (Ünvanını adı ile birlikte kullanma yetkisi olan Profesör) ve 1814 yılında Bilim Akademisi üyesi oldu. 1807 yılında Ampère ikinci kez evlendi. Ancak evlilik iki yıl sürdü. 1824 yılında Collegè de France’ta Deneysel Fizik Profesörü olan Ampère, mesleki kariyerinin zirvesine ulaştı. Ölüm onu Marsilya’ya yaptığı bir teftiş seyahati sırasında 10 Haziran 1836 günü yakaladı. Ampère’in kemikleri 1869 yılında Paris’e getirilerek Montmartre Mezarlığına gömüldü.

Ampère her şeyden önce bir matematikçiydi. Henüz 13 yaşındayken koni kesitleri üzerinde çalışmıştı. Daha sonraları olasılık hesapları üzerine ve parsiyel diferensiyal denklemler üzerine temel düşünceleri ortaya koymuştu. "Ampère Zincirleme Kanunu" daha sonraları Maxwell denklemlerinin temelini oluşturmuştu. Büyük bir dahi bilim adamı olarak kimya problemleri de onu yakından ilgilendirmişti. Ampère, atom teorisi ve fiziksel kimyanın da öncüleri arasında sayılmaktadır. Ampère 1814 yılında, basınç ve sıcaklığın da eşit olması halinde, tüm gazların eşit hacımlarda eşit sayıda moleküle sahip olacacakları hipotezini ortaya koymuştu. Ampère’in, üç yıl önce İtalyan Fizikçi Kont Amedeo Conte di Quaregna e Ceretto Avogadro’nun (1776-1856) aynı yasayı biraz değişik bir biçimde dile getirdiğinden haberi yoktu. Ampère bir matematikçi olarak, genel fizik yasalarını deneysel olarak ortaya koyup, formüllerle tespit etme yeteneğine sahipti.

Danimarkalı fizikçi Hans Christian Oersted’in (1771-1851) buluşundan hareketle, elektrik akımının, manyetizmanın nedeni olduğunu gördü. Oersted’in deneylerini devam ettirdi. Ampère yer küresinin manyetizmasının elektrik akımı geçen bir iletkeni etkilediğini düşünüyordu. 1820 yılında şamandra kuralı olarak tanımlanan kuralı ve Ampère’den bağımsız olarak bir kaç yıl sonra, Seebeck’in de açıkladığı "Selonoid" in manyetik etkisini açıkladı. Aynı yıl Ampère içinden akım geçen iki iletkenin, akımların yönü aynı olduğunda birbirlerini çektiklerini ve aksi yönde olduklarında ittiklerini kanıtladı. Böylece, daha sonraları elektrik motorlarının tasarımının gerçekleştirilmesini sağlayacak olan, elektro-mıknatısın radyal hareket oluşturmasının temel prensibi bulunmuş oldu.

Ampère daha sonra, 1822 yılında olayı matematiksel olarak tespit etti ve elektrodinamiğin temel pransiplerini bilimsel olarak ortaya koydu. Bu temel yasaya göre içinden akım geçen iki paralel iletkeni, akımların yönlerine göre, iten veya çeken kuvvet, akım ile doğru, iletkenler arsındaki mesafe ile ters orantılıdır. Ampère tarafından tespit edilen elektrodinamiğin bu temel yasası, Charles Augustin de Coulomb’un (1739-1806) elektrik yükleri ve Henry Cavendish’in (1731-1810) kitle ile ilgili yasalarına çok benziyordu.

Ampère, akan elektrik akımının manyetizmin nedeni olduğunu bulduktan sonra, atomların elektrik akımını taşıdıkları hipotezini ortaya koydu. Bundan başka, malzemelerin moleküler ring akımlarına götüren, yumuşak veya sert manyetik davranışlarını araştırdı. Ileri görüşlü bu dahinin buluşu ancak 100 yıl sonra, malzeme yapı modellerinleri üzerinde yapılan araştırmalarla, dairesel hareket eden elektronlar tarafından teyit edildi.

Elektrodinamiğin esaslarını bulmanın yanısıra, Ampère ilk elektromanyetik telgrafı da buldu. 2 Ekim 1820’de, elektrik akımı ile hareket eden bir mıknatıslı iğne ile Lyon’da telgrafla haberleşmeyi önerdi. Elektromanyetik endüksiyon onun tarafından değil, ancak 10 yıl sonra İngiliz Michael Faraday (1791-1867) bulunduğu için, onun zamanında elektrik akımının ve geriliminin ölçülmesi mümkün değildi. Ampère, Galvanometre olarak tanımladığı bir akım gösterme cihazının yaratıcısı olarak da tanınır. O aynı zamanda o zamana kadar tartışmalı olan Akım ve Gerilim kavramlarını da yerleştirdi.

André-Marie Ampère 1820-1825 yılları arasındaki çalışmalarını, 1826 yılında "Elektrodinamik Oluşumların, Yalnız Deneylerden Türetilmiş Matematiksel Teorileri Üzerine" adlı kitabında topladı. Bu ölümsüz doğa bilimleri eseri günümüzde bilinen elektrotekniğin temelini oluşturdu.

André-Marie Ampère 10 Haziran 1836’da Marsilya’da (Fransa) 62 yaşında öldü. Yaşamının son 7 yılında, onu kuvvetten düşüren, akciğer nezlesi hastalığını çekti. Fakir ve yalnız olarak ziyaret ettiği Üniversite’yi denetledikten 24 saat sonra ateş krizi bastı.

Dahi bir bilim adamı ve elektrodinamiğin kurucusu, André-Marie Ampère’in çalışmalarının ödülü, adının günümüzde birçok ölçü aletinde, cihazlarda, elektrik sayaçlarında, elektrik makinalarında, gemilerde ve caddelerde adının okunması ve onun şerefine elektrik akımı birimine adının konulmasıdır.

-------------------------------------------------------------------------

Ömer el-Hayyâm

Daha çok dörtlük biçiminde yazmış olduğu felsefî şiirlerle tanınan Ömer el-Hayyâm (1045-1123), aynı zamanda matematik ve astronomi alanlarındaki çalışmalarıyla bilimin gelişimini etkilemiş seçkin bir bilim adamıdır.

Matematiğe ilişkin araştırmaları özellikle sayılar kuramı ile cebir alanında yoğunlaşmıştır. Eukleides'in Elementler'i üzerine yapmış olduğu bir yorumda, işlemler sırasında irrasyonel sayıların da rasyonel sayılar gibi kullanılabileceğini ilk defa kanıtlamıştır.

En değerli cebir yapıtlarından birisi olan Risâle fî'l-Berâhîn alâ Mesâili'l-Cebr ve'l-Mukâbele'de (Cebir Sorunlarına İlişkin Kanıtlar) denklemlerin birden fazla kökü olabileceğini göstermiş ve bunları, kök sayılarına göre sınıflandırmıştır.

Bunun dışında, Ömer el-Hayyâm'ın üçüncü dereceden denklemleri de, terim sayılarına göre tasnif ettiği ve her grubun çözüm yöntemlerini belirlediği görülmektedir. Buna göre, üçüncü dereceden denklemler, üç terimliler ve dört terimliler olarak ikiye ayrılır ve üç terimliler,

x3 + cx2 = bx
x3 + bx = cx2
cx2 + bx = x3
olarak ve dört terimliler ise,
x3 + cx2 + bx = a
x3 + cx2 + a = bx
x3 + bx + a =cx2
cx2 + bx + a = x3 ve
x3 + cx2 = bx + a
x3 + bx = cx2 + a
x3 + a = cx2 + bx

olarak sıralanır. El-Hayyâm üçüncü derece denklemlerinin aritmetiksel olarak çözülemeyeceğine inandığı için, bu denklemleri koni kesitleri yardımıyla geometrik olarak çözmüş, negatif kökleri, daha önceki cebirciler gibi, çözüm olarak kabul etmemiştir.

Şimdi, x3 + cx2 = a denklemini nasıl çözdüğünü görelim: Yandaki şekilde, AB = c ve H3 = a olsun. AB'nin uzantısı üzerinde BT = H alınsın ve AB'ye B noktasından bir dikme çıkılsın. BC = H olsun ve BCDT k****i tamamlansın. BCDT k****i üzerine H yüksekliğine sahip bir küp çizilsin. D köşesinden, asimptotları BC ve BT olan EDN hiperbolü ve A köşesinden, AT eksenli ve BC parametreli AK parabolü çizildiğinde, bu hiperbol ile parabol kesişmek zorundadırlar. Kesişme noktaları E olsun. E'den AT ve BC doğrularına iki dikme inilsin ve bunlar EZ ve EL olsun. Bu durumda x = BZ olacaktır.

Kanıt : EZ2 = AZ . BC (parabolün özelliğinden) *

(AZ/EZ)=(EZ/BC)

EZ . BZ = BC . BT = BC2 (hiperbolün özelliğinden)

(BZ/BC) = (BC/EZ) olur ve ikinci ifadenin k****i alınırsa,

((BZ)2 /(BC)2) = ((BC)2 / (EZ)2) elde edilir.

AZ = BZ + AB olduğuna göre, BC3 = BZ2 (BZ + AB) = (BZ3 + BZ2). AB) elde edilir. BC = H, H³ = a, AB = c olarak verildiğinden, a = (BZ3 + c . BZ2 ) bulunur. BZ yerine x konursa, orijinal denklem elde edilecektir; öyleyse BZ = x olmalıdır.

Ömer el-Hayyâm'ın astronomi alanındaki çalışmaları da çok önemlidir. Eskiden beri kullanılmakta olan takvimlerin düzeltilmesi için Selçuklu Sultanı Celâleddin Melikşâh (1052-1092), 1074-1075 yılları civârında İsfahan'da bir gözlemevi kurdurmuş ve başına da dönemin en ünlü astronomlarından biri olan Ömer el-Hayyâm'ı getirmişti. Ömer el-Hayyâm ile arkadaşlarının yapmış olduğu araştırmalar sonucunda, daha önce kullanılmış olan takvimleri düzeltmek yerine, mevsimlere tam olarak uyum gösterecek yeni bir takvim düzenlemenin daha doğru olacağına karar verilmiş ve bu maksatla gözlemler yapılmaya başlanmıştır. Gözlemler tamamlandığında, hem Zîc-i Melikşâhî (Melikşâh Zîci) adlı zîc ve hem de et-Târîhu'l-Celâlî denilen Celâleddin Takvimi düzenlenmiştir (1079). Celâleddin Takvimi, bugün kullanmakta olduğumuz Gregorius Takvimi'nden çok daha dakiktir; Gregorius Takvimi, her 3330 yılda bir günlük bir hata yaptığı halde, Celâleddin Takvimi 5000 yılda yalnızca bir günlük hata yapmaktadır.

---------------------------------------------------------------------------------

Descartes

Modern felsefenin ve analitik geometrinin kurucusu olan Descartes (1596 - 1650) için de, Bacon'da olduğu gibi, amaç doğayı egemenlik altına almaktır. Çünkü insan ancak o zaman mutlu olabilir. Fakat doğa, skolastiğin sağladığı bilgilerle egemenlik altına alınamaz. Böylece Descartes'ın da skolastiğin insanı yanlışa götürdüğünü düşündüğü anlaşılmaktadır. Ona göre, bunun iki nedeni vardır.

1-Skolastiğin kavramları açık ve seçik değildir.
2-Bu yöntem doğru bilgi elde etmeye uygun değildir.

Böylece Descartes yeni bir yönteme gereksinim olduğunu belirtir. Çünkü ona göre doğruyu yanlıştan ayırt etme gücü, yani akıl (sağduyu) eşit olarak dağıtılmıştır. O halde bu kadar yanlış bilginin kaynağı akıl olamaz. Böylece Descartes, insanların yanlışa düşmelerinin tek nedeninin doğru bir yönteme sahip olmamaları olduğu sonucunu çıkarır.

Bundan sonra yöntemini kurmaya çalışan Descartes, öncelikle bu konuda kendine nelerin yardımcı olacağını araştırır ve iki şeyin bulunduğuna karar verir:
1-Klasik mantık
2-Eskilerin kullandığı Analiz

Descartes, eskiden beri kullanmakta olan bu iki yöntemden klasik mantığın, bilinenleri başkalarına öğretmekte, genç zekaları çalıştırmakta ve onlara bir disiplin kazandırmakta yararlı olduğunu, ancak yeni bir bilgi elde etmekte işe yaramadığını belirtir. Çünkü ona göre, bu mantıkta biçim ve içerik ayrılmıştır. Oysa ki bilgide biçim ve içerik iç içedir.

Eskilerin kullandığı analize gelince, Descartes, Platon'dan beri eskilerin matematiğin en yalın bilim olduğunu ve diğer bilimlerin temelinde yer aldığını, fakat kendi dönemindeki matematiğin bu özellikten yoksun bulunduğunu belirtir. Bunun üzerine eskilerin matematik çalışmalarını incelemeye koyulur ve Papus'un Matematik Koleksiyonları adlı kitabında kanıtlamanın iki boyutundan söz edildiğini belirler. Bunlar analiz ve sentezdir.

Descartes bu iki yoldan analizin daha doğru olduğuna karar verir. Matematikle ilgili çalışmaları sonucunda da analitik geometriyi bulur. Burada esas olan bir cebir denkleminin bir geometrik şekille anlatılmasıdır. Descartes'ın bu önemli buluşundan sonra diğer önemli bir katkısı da geometri ile cebir arasında kurduğu paralelizmin aynı şekilde matematik ve diğer bilimler arasında da kurulabileceğini belirtmesidir. Çünkü ona göre her hangi bir bilimde bir şeyi bilmek demek aslında sayı ve ölçüden başka bir şey değildir. Bundan dolayı da bütün bilimlerde tek bir yöntem uygulamak olanaklıdır. Bu da matematiksel yöntemdir. Böylece ilk defa bütün bilimlerin yönteminin tek bir yöntem olduğu belirtilmiştir. Bu nedenle Descartes'ın yöntemine evrensel matematik yöntem denmiştir.

Descartes bu yöntemini dört kuralla temellendirmiştir.
1-Apaçıklık Kuralı: Doğruluğu apaçık bilinmeyen hiçbir şeyi doğru olarak kabul etmemek, yani acele yargılara varmaktan ve ön yargılara saplanmaktan çekinmek, yargılarda ancak kendilerinden kuşkulanılmayacak derecede açık ve seçik olarak kavranılan şeyleri bulundurmak.

Bu kuralda dikkat çeken en önemli yön insanın bir konuyu araştırmaya başlarken, ön yargısız davranmasının gerekliliğidir. Bu ise oldukça zordur. Çünkü insan hem doğuştan getirdiği, hem de yaşamı boyunca edindiği pek çok ön yargıya sahiptir. Bunu aşmak ise çok zordur. Ancak Descartes bunun için yöntemsel kuşkuculuk'u önerir

Bu yöntemin esası, sağlam bir nokta buluncaya kadar sezişle apaçık olarak kavranılamayan her şeyden kuşku duymaktır. Bu yönüyle kuşkucuların yöntemlerinden tamamen farklı olan yöntemsel kuşkuculuk, Descartes'ın deyimiyle, gerçeği, yani kayayı bulmak için gevşek toprak ve kumu atmak amacına dayanır. Böylece elde edilen bilgi artık kendisinden kuşku duyulmayan, apaçık olarak kavranılan, doğruluğuna güvenilen bilgi olacaktır.

2-Analiz Kuralı: Bu kural incelenecek problemlerden her birini, olanaklar ölçüsünde ve daha iyi çözümlemek için gerektiği kadar parçalara ayırmayı belirtir, yani karmaşık ve karanlık olan önermelerden, basamak basamak daha yalın önermelere inmek ve daha sonra bu yalın önermelerden başlayarak daha karmaşıkların bilgisini elde etmektir.

3-Sıra Kuralı: En yalın ve bilinmesi en kolay şeylerden başlayarak, tıpkı basamak basamak bir merdivenden çıkar gibi, derece derece daha karmaşık olanların bilgisine yükselirken, doğaları gereği ard arda sıralanmayan şeyler arasında bile bir sıra olduğunu öngörerek düşünmeyi yürütmektir.

4-Sayış kuralı: Bu kural hiçbir şeyin unutulup atlanmadığından emin olmak için, her yönden tam sayış ve genel tekrar yapmayı belirtir. Burada dikkat edilmesi gereken dört nokta vardır. Sayışın sürekli, kesiksiz, yeter ve sıralı olması.

Descartes'ın bu analiz ağırlıklı, yöntemsel kuşkuculuğa dayanan yöntemi, felsefe için gerçekten çok yenidir. Bu anlamda o, modern felsefenin kurucusu kabul edilmiştir. Ancak onun bu başarısını bilimde de gösterdiğini söylemek zordur. Çünkü bilim anlayışında önemli yanlışlar vardır. Aslında bilimlere matematiğin uygulanabileceğini belirtmesi önemlidir. Örneğin fiziği matematiğe, daha doğrusu geometriye indirgemeye çalışması yanlıştır. Çünkü modern bilim anlayışında bilimlerin inceleme alanlarını geometrik nesnelere indirgemek, yani yalnızca yayılım olarak düşünmek olanaksızdır. Bundan dolayı da, Descartes'ın anladığı anlamda matematiksel yöntem bilimlerde başarıyla uygulanamaz.

Bilimin yöntemi ve kartezyen felsefe sistemiyle ünlü olan Descartes, aynı zamanda büyük bir matematikçidir. Cebirsel işlemleri geometriye uygulayarak analitik geometriyi kurmuştur. O zamana kadar geometri ve cebir problemleri kendi özel yöntemleri ile ayrı ayrı çözülmekteydi. Ancak Descartes, cebir ve geometri arasındaki bu mesafeyi ortadan kaldıran, cebiri geometriye uygulayan genel bir yöntem ileri sürdü. Descartes'ın bu yönteminin iki amacı vardı:

1. Cebirsel işlemlerle, geometriyi şekil kullanımından kurtarmak.
2. Cebir işlemlerine geometrik yorumlarla anlam kazandırmak.
Descartes bu bağlamda, ilk defa koordinat geometrisi fikrini şekil de görüldüğü gibi ifade etti.

Buna göre, ox ve oy doğruları, o noktasında (orijinde) birbirlerini dik olarak keserler. Bu doğrular, aynı düzlemde bulunan bir P noktasının konumunu belirlemek için eksenler olarak kullanılır. P noktasının konumu, eksenler üzerinde OM=x ve PM=y uzaklıkları ile belirlenir. Yani P(x,y) noktasının tanımlanabilme koşulu x ve y gibi iki parametre yardımıyla sağlanmaktadır. x ve y uzaklıklarına P noktasının koordinatları denir. x ve y arasındaki farklı münasebetler aynı düzlemde farklı eğrilere tekabül eder. Böylece, eğer y, x ile orantılı olarak büyürse, yani y=kx olursa, bir doğru parçasını ve y=kx2 olursa, bir parabolü temsil eder. Bu tür denklemler cebirsel olarak çözülebilir ve bulunan neticeler geometrik olarak yorumlanabilir. Bu şekilde, daha önce çözülemeyen ya da çok güçlükle çözülebilen pek çok fizik probleminin çözümü bundan sonra (örneğin Newton'da) mümkün olmuştur.

Descartes bütün fiziğin bu şekilde geometrik ilişkilere indirgenebileceğini düşünerek, bütün evreni matematiksel olarak açıklamaya çalışmıştır.

Descartes fizik ve evrenbilimle de ilgilenmiş ve 1644 yılında yayımladığı Principia Philosophia (Felsefenin İlkeleri) adlı Latince yapıtında ileri sürmüş olduğu Çevrimler Kuramı ile Newton'dan önce evrenin yapısı ve işleyişine ilişkin mekanik bir açıklama getirmişti; bu yapıt, daha sonra Fransızca'ya çevrildi ve Avrupa düşüncesi üzerinde çok etkili oldu.

Aristotelesçi hareket düşüncesi, gezegenleri yöneten gücün, aynı zamanda onları ileriye doğru sürükleyen güç olduğunu benimsiyordu. Aslında Yunan Mitolojisi'ne, yani bir savaş arabası ile atlarla donanmış Apollon (Güneş) tasarımına dayanan bu inanç Hıristiyan Mitolojisi tarafından da benimsenmiş, ancak atların yerine meleklerin gücü geçirilmişti. Diğer taraftan 16. yüzyılın önde gelen gökbilimcilerinden Tycho Brahe ve yandaşları, Aristotelesçi Evren Kuramı'na sonradan eklenen ve gökcisimlerini taşıdıklarına inanılan saydam ve katı kürelerin bulunmadığını gözlemsel olarak kanıtlamışlar ve böylece büyük bir sorunun doğmasına sebebiyet vermişlerdi: Şâyet gökcisimlerini saydam ve katı küreler taşımıyorsa, ne taşıyordu? Mekanik oluşumları, maddenin madde üzerindeki etkisiyle açıklamak gerektiğini düşünen Descartes, uzayın boş olmadığı görüşüyle birlikte, bir cismin devinebilmesi için gerekli olan kuvvetin başka bir cisim tarafından sağlanması gerektiği görüşünü de gelenekten almıştı; fakat artık atları ve melekleri kullanmıyordu. Bütün gezegenlerin, akışkan özdekle dolu bir uzayda oluşan çevrimlerin, yani girdapların veya hortumların merkezinde bulunduğunu savunuyordu. Bu çevrimlerin dönüşü, merkezlerinin yakınında çok hızlıydı ve gezegenlerin eksenleri çevresinde dönmelerini sağlıyordu. Çevrimlerin dış kısımları ise, gezegenlerin sahip oldukları uyduları dolandırıyordu. Yerel gezegensel çevrimler, merkezinde Güneş'in bulunduğu daha geniş bir çevrimin içine oturmuştu; öyle ki bu çevrim, gezegenleriyle birlikte diğer çevrimlerin düzenli bir biçimde Güneş'in çevresinde dolanmasını sağlıyordu.

Bu kuram çok akıllıca ve ilk bakışta çok çekiciydi; çünkü başka olguların yanında Yersel dönüş sırasında neden güçlü hava akımlarının oluşmadığını ve küçük cisimlerin neden Yersel çevrim merkezine doğru gittiklerini veya düştüklerini açıklayabiliyordu.

Bir varsayım, öndeyilerinin doğruluğu ile yargılanmalı ve değerlendirilmelidir. Descartes'ın varsayımının güçsüzlüğü, matematiksel olarak işlenememesi ve bu nedenle yeterli düzeyde denetlenememesi ve sorgulanamamasından kaynaklanıyordu; ama matematiksel olarak gösterilemediği için denetlenmesi ve sınanması olanaksızdı. Akışkanların devinimine ilişkin sorunlar, 17. yüzyıl matematiğinin dışında kalıyordu. Descartes'ın varsayımından yararlanarak, Güneş'e daha yakın olan gezegenlerin daha hızlı hareket etmeleri gerektiğini öngörmek olanaklıydı; fakat gezegenlerin uzaklıkları ile dolanım süreleri, yani periyotları ararsında bulunması gereken kesin ilişkiyi ve bağlantıyı öngörmek olanaksızdı. Ayrıca, karmaşık bir çevrimler dizgesinde, bir gezegenin çizdiği yörüngenin biçimini öngörmek de mümkün değildi. Gezegen devinimlerine ilişkin yasalar, Kepler tarafından matematiksel bir kesinlikle ortaya konulmuştu ve artık Kepler Yasaları'nın kendisinden çıkarsanacağı doyurucu bir mekanik kurama gereksinim duyulmaktaydı; bulanık ve niteliksel bir biçimde gezegen devinimlerinin temel özellikleriyle ilgilenen kuramlar, artık ömürlerini tamamlamışlardı.

---------------------------------------------------------------------------------
Thales

Bu okulun ilk temsilcisi olan Thales M.Ö. 624 yılında doğmuş ve M.Ö. 548 yılında ölmüştür. Varlıklı bir tacirdi. Yunanlı yedi bilgeden birisi olarak kabul edilmekteydi. Thales ile ilgili şu hikaye kayıtlara geçmiştir. Lidyalılarla Persler arasında uzun süren bir savaş sırasında, 28 Mayıs 585 tarihinde, Güneş'in tutulacağını önceden bildirmiş ve bu olaydan çok etkilenen iki kral derhal bu savaşa son vermişlerdir. Bu hikaye, ilk bakışta inanılmaz gibi görünmekteyse de, şu noktayı göz ardı etmemek gerekir: Babilliler, Güneş tutulmasını önceden bildirme olanağını veren Saros Periyodu'nu biliyorlardı. Söylendiğine göre, Thales Mısır'a gittiğinde bunu öğrenmişti. Ayrıca Mısır'da 603 yılındaki Güneş tutulmasını ya bizzat görmüş ya da Mısırlılardan işitmişti. 18 yıl 11 gün sonra, başka bir tutulmanın daha olacağı hesaplanabilirdi ve bu tutulma da 585 yılına rastlıyordu.

İlk Yunan matematikçisi Thales'tir. Proklos, Thales'e ilişin olarak şunları söyler :

"İlk önce Mısır'a gitti ve bu çalışmaları (geometriyi) Yunanlılara tanıttı. Bizzat kendisi, pek çok temel önerme keşfetti; diğer prensiplerin ışığı altında, onları kendisinden sonra gelenlere öğretti. Onun yöntemi daha genel (daha kuramsal ve daha bilimsel), diğerlerinin yöntemleri ise daha emprikti."

Thales'le birlikte geometri ilk defa dedüktif (yani tümdengelimsel) bir bilim dalı haline geldi. Buna ilişkin olarak Plutarkos, Yedi Bilge adlı yapıtında şunları söyler :

"Görünen şudur ki Thales, aklıyla pratik yararın ötesine geçip, akıl yürütmeye girişenlerden birisidir. Geri kalanlar aklın ününü, politikada arayanlardır."

Thales'in bir piramidin yüksekliğini nasıl ölçmüş olduğuna ilişkin söylentiler çok değişiktir. Bunlardan en yalını Aristoteles'in bir öğrencisi olan Hieronymus'a aittir. Onun açıklamaları, Diogenes Laertius tarafından şöyle anlatılır :

"Hieronymus, Thales kendi gölgesinin, kendi boyuna eşit olduğu anda, piramidin gölgesini ölçerek yüksekliğini bulmuştur demektedir."

Bu yaklaşımıyla, Thales bir cismin gölgesinin, kendi boyuna eşit olduğu bir anda, diğer bütün cisimlerin gölgelerinin de, kendi boylarına eşit olacağı sonucuna ulaşmış oluyordu. Thales'in kullandığı bu yöntem, Mısırlıların kullandıkları se get hesabından başka bir şey değildir. Bu yöntem 57 numaralı Ahmes papirüsünde açıklanmıştır.

Thales, bir geminin kıyıdan ne kadar uzak olduğunun ölçülmesi ile de ilgilenmiştir. Bu ölçümü, iki dik üçgenin kenarları arasındaki orantıdan yararlanarak yapmıştır. B, şekildeki (şekil 4) kulenin tabanı, C ise gemi olsun. Bir kimse kulenin tepesinde, elinde birbirini dik açıyla kesen bir araç bulundursun. Onun bir kenarı olan AD, Yer'e dik bir konumda bulunsun. AE kenarı ise gemi yönünde olsun. Sonra öyle bir gözlem noktası saptansın ki, bu noktadan C gemisi görülebilsin. AC doğrusu, E noktasında, aracın yatay kolunu keser. AD = 1, DE = m ve BD = h denilecek olursa, BC doğrusu, yani geminin karaya olan uzaklığı, BC = (h * 1) . m / 1 olur.

(Thales teoremi uygulanarak BCE=ADB, BC = (AD / DB). DE elde edilir.)

Aşağıdaki geometrik öneriler ona atfedilmektedir :
1. Yarıçap, daireyi iki eşit parçaya böler.
2. İkizkenar bir üçgenin tabanına komşu olan açılar eşittir.
3. İki doğru kesiştiğinde karşıt açılar eşittir.
4. Yarım daireyi gören açılar diktir.
5. İkişer açısı ve birer kenarları eşit olan üçgenler birbirlerine eşittir.

Thales, eşit açı yerine benzer açı deyimini kullanmaktadır; bundan da açıyı nicel bir büyüklük olarak değil, bir şekil olarak düşündüğü sonucu çıkmaktadır.

Bunların kanıtlamalarını yapabiliyor muydu? Eşit oldukları sonucuna nasıl ulaşmıştı? Bu soruların yanıtını bulmak olanaksızdır. Ancak tarihte geometrik önerilerin gerekliliğine inanan ilk kişi Thales'tir.

Thales aynı zamanda astronomiyle de ilgilenmiş ve tarih kitaplarına ilk Yunan astronomu olarak geçmiştir. Gökyüzündeki yıldızları gözlemlerken bir kuyuya düştüğünü herkes bilir. 28 Mayıs 585 yılında gerçekleşen Güneş tutulmasını daha önceden tahmin etmiş olmasına rağmen, Yer'in bir disk biçiminde olduğunu düşündüğünden, Ay ve Güneş tutulmalarının nedenlerini bilmesi olanaksızdı.

Mısırlılardan yılın 365 gün olduğunu öğrenmişti. Kuzey yönünün bulunmasında Küçük Ayı'nın kullanılabileceğini biliyordu ve Yunan gemicilerine Küçük Ayı takım yıldızını gözlemleyerek seyahat etmelerini önermişti. Nitekim denizci bir millet olan Fenikeliler de Büyük Ayı'yı kullanıyorlardı.

Thales her şeyin aslının su olduğunu söylüyordu; su, katı, sıvı ve gaz olmak üzere üç durumda bulunabilirdi. Suyun olmadığı yerde hayatın da olmayışı, bu maddenin aslî oluşunun en güçlü kanıtlarından biriydi. Thales, bu görüşleri ve Homeros'un hikayelerini bir yana bırakan gözlemsel düşünceleri nedeniyle bilimin doğuşunda önemli bir rol oynamıştır.

Aristoteles'e göre, Thales, mıknatısın demir tozlarını çekmesi nedeniyle canlı olduğuna inanıyordu. Nasıl bir yorum getirirse getirsin, mıknatıstan söz eden ilk kişi de Thales'ti.

---------------------------------------------------------------------------------
Sokrates

Bütün insanlık tarihinin en saygın kişilerinden birisi olarak tanınan Sokrates de aslında bir sofisttir. Atina'da doğmuş (M.Ö. 470) ve iyi bir eğitim görmüştür. Babası, onu kendi mesleğinde, yani bir heykeltıraş olarak yetiştirmek istediği halde, Sokrates felsefeye ilgi duymuştur. Meydanlarda, tiyatrolarda ve yollarda felsefî tartışmaların yapıldığı bir ortam içinde böyle bir istek gayet doğaldı. Sokrates, aritmetik, geometri, astronomi ve politikaya ilişkin yeterli düzeyde bilgiye sahipti. Çok basit bir yaşam sürmüştü. Her ne kadar görüşlerinin çok etkili olduğu kabul edilmişse de, hiçbir yapıt kaleme almamıştır. Onu iki öğrencisi, Platon ve Ksenofanes'in yazdıklarından tanımaktayız.

Sokrates diğer sofistlerden çok farklıydı. Düzenli bir öğretim yapmıyor ve öğrencilerinden ücret almıyordu. "Kendini bil!" ilkesi doğrultusunda, düşünürlerin bakışlarını evrenden insana çevirmişti. Evreni anlamlandırmadan önce kendimizi anlamlandıralım; "Biz kimiz?" bu sorunun yanıtını verelim diyordu. Bu nedenle, yalnızca bir tarlayı ölçebilecek düzeydeki geometri bilgisini yeterli buluyor, daha zor matematik problemleriyle uğraşmanın yararsız olduğuna işaret ediyordu. Ona göre, insanlara, pratik ahlak kurallarını öğretmek daha isabetli olacaktı. Böylece Sokrates, kuramsal bilim ve uygulamalı bilim tartışmasını da açmış oluyordu.

Sokrates ilk anlambilimcidir; anlamları belirlenmemiş kavramların ve terimlerin kullanılmasının sakıncalarına temas etmiştir. Her çeşit bilgide, kavramların ve terimlerin açık ve seçik bir biçimde tanımlamalarının yapılması gerektiğini savunmuş olması, dolaylı yoldan da olsa, bilimin ilerlemesine küçümsenemeyecek ölçüde katkıda bulunmuştur.Beş kitaptan oluşan bu ansiklopedik eserin Birinci Kitab'ı, anatomi ve koruyucu hekimlik, İkinci Kitab'ı basit ilaçlar, Üçüncü Kitab'ı patoloji, Dördüncü Kitab'ı ilaçlarla ve cerrâhî yöntemlerle tedavi ve Beşinci Kitab'ı ise çeşitli ilaç terkipleriyle ilgili ayrıntılı bilgiler vermektedir.

İslam tarihinde önemli adımların atıldığı bir dönemde bilim hususunda daha sonra gelişecek olan Avrupa biliminde de önemli etkileri olacak olan İbn Sina, geliştirdiği felsefeyle de daha sonraları bir çok İslam alimi tarafından da eleştirilmiştir.

----------------------------------------------------------------------------------

Georg Friedrich Bernhard Riemann (17 Eylül 1826 - 20 Temmuz 1866)

Analiz ve diferansiyel geometri dalında çok önemli katkıları olan Alman matematikçidir. Söz konusu katkılar daha sonra izafiyet teorisinin geliştirilmesinde önemli rol oynamıştır. Bu matematikçinin ismi aynı zamanda zeta fonksiyonu, Riemann hipotezi, Riemann manifoldları ve Riemann yüzeyleri ile de bağlantılıdır.

Almanya'da Dannenberg yakınlarındaki Hanover Krallığının Breselenz kasabasında doğan matematikçinin babası Friedrich Bernhard Riemann idi. Bernhard Riemann altı çocuklu bir ailenin ikinci çocuğuydu.

Riemann, 1840 yılında büyükannesi ile yaşamak ve Lyceum'u ziyaret etmek için Hanover'e gitti. Büyükannesinin 1842 yılındaki vefatından sonra Lüneburg'daki Johanneum'a giden Riemann, 1846 da yani 19 yaşında Göttingen Üniversitesi'nde filoloji ve teoloji çalışmaya başladı. En küçük kareler yöntemini anlatan matematikçi Gauss'un derslerine katıldı. 1847 yılında Riemann'ın babası ona teolojiyi bırakıp matematik çalışması için izin verdi.

1847 yılında Berlin'e gitti. Burada Jacobi, Dirichlet veya Steiner ders veriyordu. Berlin'de iki yıl kalan matematikçi 1849 yılında Göttingen'e döndü.

Riemann ilk dersini 1854'te verdi ve bu dersle sadece Riemann geometrisinin temellerini kurmakla kalmadı aynı zamanda daha sonra Einsteinin izafiyet teorisinde kullanacağı yapıların da temellerini attı. 1857'de Götingen Üniversitesi'nde özel profesörlük kademesine terfi etti ve 1859'da profesör oldu.

1862 yılında Elise Koch ile evlendi.

Selasca, İtalya'ya doğru gerçekleştirdiği üçüncü seyahatte hayata gözlerini yumdu.

Georg Friedrich Bernhard Riemann (17 Eylül 1826 - 20 Temmuz 1866), analiz ve diferansiyel geometri dalında çok önemli katkıları olan Alman matematikçidir. Söz konusu katkılar daha sonra izafiyet teorisinin geliştirilmesinde önemli rol oynamıştır. Bu matematikçinin ismi aynı zamanda zeta fonksiyonu, Riemann hipotezi, Riemann manifoldları ve Riemann yüzeyleri ile de bağlantılıdır.

Almanya'da Dannenberg yakınlarındaki Hanover Krallığının Breselenz kasabasında doğan matematikçinin babası Friedrich Bernhard Riemann idi. Bernhard Riemann altı çocuklu bir ailenin ikinci çocuğuydu.

Riemann, 1840 yılında büyükannesi ile yaşamak ve Lyceum'u ziyaret etmek için Hanover'e gitti. Büyükannesinin 1842 yılındaki vefatından sonra Lüneburg'daki Johanneum'a giden Riemann, 1846 da yani 19 yaşında Göttingen Üniversitesi'nde filoloji ve teoloji çalışmaya başladı. En küçük kareler yöntemini anlatan matematikçi Gauss'un derslerine katıldı. 1847 yılında Riemann'ın babası ona teolojiyi bırakıp matematik çalışması için izin verdi.

1847 yılında Berlin'e gitti. Burada Jacobi, Dirichlet veya Steiner ders veriyordu. Berlin'de iki yıl kalan matematikçi 1849 yılında Göttingen'e döndü.

Riemann ilk dersini 1854'te verdi ve bu dersle sadece Riemann geometrisinin temellerini kurmakla kalmadı aynı zamanda daha sonra Einsteinin izafiyet teorisinde kullanacağı yapıların da temellerini attı. 1857'de Götingen Üniversitesi'nde özel profesörlük kademesine terfi etti ve 1859'da profesör oldu.

1862 yılında Elise Koch ile evlendi.

Selasca, İtalya'ya doğru gerçekleştirdiği üçüncü seyahatte hayata gözlerini yumdu.
---------------------------------------------------------------------------------

Pierre de Fermat (piyer dö ferma okunur) (d. 1601, Beaumont-de-Lomagne – ö. 12 Ocak 1665, Castres)

Bask kökenli Fransız hukukçu ve matematikçi. İlk öğrenimini doğduğu şehirde yapmıştır. Yargıç olmak için çalışmalarına Toulouse’de devam etmiştir. Fermat, memurluğunun yoğun işlerinden geriye kalan zamanlarında matematikle uğraşmıştır. Arşimet'in eğildiği diferansiyel hesaba geometrik görünümle yaklaşmıştır. Sayılar teorisinde önemli sonuçlar bulmuş, olasılık ve analitik geometriye de katkılarda bulunmuştur.

Günümüzde hatırlanmasının en önemli sebebi Fermat'nın Son Teoremi(ayrıntı için tıkla)'dir. Modern sayılar kurucusu olarak kabul edilen 17. yüzyıl matematikçisi Pierre de Fermat'nın adını taşıyan bu teorem, şu şekilde ifade edilebilir:

Herhangi x, y, ve z pozitif tam sayıları için,

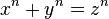
$x^n + y^n = z^n ;$

ifadesini sağlayan ve 2'den büyük bir doğal sayı n yoktur. Fermat, bu problemi çözmüş, kanıtı da Eski Yunanlı matematikçi Diaphontos Arithmetika adlı kitabının kendindeki kopyasının sayfalarından birinin kenarına 1637 de şöyle yazmıştı:

x, y, z ve n pozitif tamsayılar ve n>2 olmak koşuluyla, x^n + y^n = z^n denkleminin çözümü yoktur. Ben bunun kanıtını buldum, ama kanıtı bu kenar boşluğuna sığdırmak olanaksız.

Ancak bu kanıt bulunamamıştır. Fermat'tan sonra matematikçiler bu önermenin bir türlü içinden çıkamamışlardır. Fermat'ın bıraktığı defterler arasında teoremin kanıtına rastlayamadıkları gibi, kendileri de ne doğruluğunu ne yanlışlığını kanıtlayabilmişlerdir. Yıllar boyunca (300 yıl sonrasına kadar) bu konuda yapılan çalışmalar sonucu bu teoremin Shimura-Taniyama Konjektürü'nün bir özel durumu olduğu anlaşılmış, ardından da 1993'te İngiliz matematikçi Andrew Wiles, eski öğrencilerinden Richard Taylor'ın da yardımıyla ve cebirsel geometrinin çok karmaşık araçlarını kullanarak teoremi kanıtlamanın bir yolunu bulmuş ve bu kanıtı 1995'te Annals of Mathematics adlı dergide yayımlamıştır. Shimura-Taniyama Konjektürü'nün böylelikle ispatlanması sonucu Fermat'nın Son Teoremi de 1995'te ispatlanmış oldu.

Asal sayılar üzerinde çok durmuştur. Onun bu konuda çeşitli teoremleri vardır. Örneğin,

$4 n + 1$

şeklinde yazılan bir asal sayı p, yalnızca bir tek şekilde iki karenin toplamı olarak yazılabilir.

$p = a^2 + b^2 iff p = 4n + 1$

Mesela en ufak asal sayılar p:

$5 = 1 2 + 2 2$ ve $13 = 2 2 + 3 2$

dir. Bu teoremi daha sonra Euler kanıtlamıştır.

Pierre de Fermat (piyer dö ferma okunur) (d. 1601, Beaumont-de-Lomagne – ö. 12 Ocak 1665, Castres), Bask kökenli Fransız hukukçu ve matematikçi. İlk öğrenimini doğduğu şehirde yapmıştır. Yargıç olmak için çalışmalarına Toulouse’de devam etmiştir. Fermat, memurluğunun yoğun işlerinden geriye kalan zamanlarında matematikle uğraşmıştır. Arşimet'in eğildiği diferansiyel hesaba geometrik görünümle yaklaşmıştır. Sayılar teorisinde önemli sonuçlar bulmuş, olasılık ve analitik geometriye de katkılarda bulunmuştur.

Günümüzde hatırlanmasının en önemli sebebi Fermat'nın Son Teoremi(ayrıntı için tıkla)'dir. Modern sayılar kurucusu olarak kabul edilen 17. yüzyıl matematikçisi Pierre de Fermat'nın adını taşıyan bu teorem, şu şekilde ifade edilebilir:

Herhangi x, y, ve z pozitif tam sayıları için,

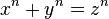
$x^n + y^n = z^n ;$

ifadesini sağlayan ve 2'den büyük bir doğal sayı n yoktur. Fermat, bu problemi çözmüş, kanıtı da Eski Yunanlı matematikçi Diaphontos Arithmetika adlı kitabının kendindeki kopyasının sayfalarından birinin kenarına 1637 de şöyle yazmıştı:

x, y, z ve n pozitif tamsayılar ve n>2 olmak koşuluyla, x^n + y^n = z^n denkleminin çözümü yoktur. Ben bunun kanıtını buldum, ama kanıtı bu kenar boşluğuna sığdırmak olanaksız.

Ancak bu kanıt bulunamamıştır. Fermat'tan sonra matematikçiler bu önermenin bir türlü içinden çıkamamışlardır. Fermat'ın bıraktığı defterler arasında teoremin kanıtına rastlayamadıkları gibi, kendileri de ne doğruluğunu ne yanlışlığını kanıtlayabilmişlerdir. Yıllar boyunca (300 yıl sonrasına kadar) bu konuda yapılan çalışmalar sonucu bu teoremin Shimura-Taniyama Konjektürü'nün bir özel durumu olduğu anlaşılmış, ardından da 1993'te İngiliz matematikçi Andrew Wiles, eski öğrencilerinden Richard Taylor'ın da yardımıyla ve cebirsel geometrinin çok karmaşık araçlarını kullanarak teoremi kanıtlamanın bir yolunu bulmuş ve bu kanıtı 1995'te Annals of Mathematics adlı dergide yayımlamıştır. Shimura-Taniyama Konjektürü'nün böylelikle ispatlanması sonucu Fermat'nın Son Teoremi de 1995'te ispatlanmış oldu.

Asal sayılar üzerinde çok durmuştur. Onun bu konuda çeşitli teoremleri vardır. Örneğin,

$4 n + 1$

şeklinde yazılan bir asal sayı p, yalnızca bir tek şekilde iki karenin toplamı olarak yazılabilir.

$p = a^2 + b^2 iff p = 4n + 1$

Mesela en ufak asal sayılar p:

$5 = 1 2 + 2 2$ ve $13 = 2 2 + 3 2$

dir. Bu teoremi daha sonra Euler kanıtlamıştır.